题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由![]() 平面
平面![]() ,可得到
,可得到![]() ,结合
,结合![]() ,根据线面垂直的判定定理即可得到
,根据线面垂直的判定定理即可得到![]() 平面
平面![]() ,从而可得出
,从而可得出![]() ;(2)首先以
;(2)首先以![]() 三直线为
三直线为![]() 轴,建立空间直角坐标系,可设
轴,建立空间直角坐标系,可设![]() ,从而可确定图形上各点的坐标,利用向量垂直数量积为零列方程组求出平面
,从而可确定图形上各点的坐标,利用向量垂直数量积为零列方程组求出平面![]() 的法向量,设直线
的法向量,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则根据
,则根据![]() 及空间向量夹角余弦公式,即可求得
及空间向量夹角余弦公式,即可求得![]() .
.
试题解析:(1)![]() 平面
平面![]() 平面
平面![]() ,即
,即![]() ,又
,又![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
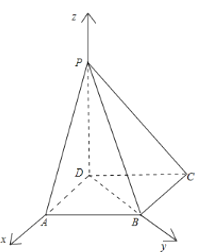
(2)分别以![]() 三直线为
三直线为![]() 轴,建立如图所示空间直角坐标系,设
轴,建立如图所示空间直角坐标系,设![]() ,则
,则![]() ,
,![]() ,
,![]()
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则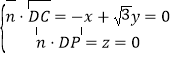 ,取
,取![]() ,记直线
,记直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,
,![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查线面垂直的判定与性质,以及利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
在所给的坐标图纸中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;

(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?