题目内容
【题目】给定一个数列{an}，在这个数列里，任取m（m≥3，m∈N*）项，并且不改变它们在数列{an}中的先后次序，得到的数列{an}的一个m阶子数列．
已知数列{an}的通项公式为an= 
（n∈N* ， a为常数），等差数列a2 ， a3 ， a6是数列{an}的一个3子阶数列．
（1）求a的值；
（2）等差数列b1 ， b2 ， …，bm是{an}的一个m（m≥3，m∈N*）阶子数列，且b1= 
（k为常数，k∈N* ， k≥2），求证：m≤k+1
（3）等比数列c1 ， c2 ， …，cm是{an}的一个m（m≥3，m∈N*）阶子数列，求证：c1+c1+…+cm≤2﹣ 
．
【答案】
（1）解：∵a2，a3，a6成等差数列，
∴a2﹣a3=a3﹣a6．
又∵a2= 
，a3= 
，a6= 
，
代入得 ﹣ = ﹣ ，解得a=0
（2）证明：设等差数列b1，b2，…，bm的公差为d．
∵b1= 
，∴b2≤ 
，
从而d=b2﹣b1≤ ﹣ =﹣ 
．
∴bm=b1+（m﹣1）d≤ ﹣ 
．
又∵bm＞0，∴ ﹣ ＞0．
即m﹣1＜k+1．
∴m＜k+2．
又∵m，k∈N*，∴m≤k+1．
（3）证明：设c1= 
（t∈N*），等比数列c1，c2，…，cm的公比为q．
∵c2≤ 
，∴q= 
≤ 
．
从而cn=c1qn﹣1≤ 
（1≤n≤m，n∈N*）．
∴c1+c2+…+cm≤ + 
+ 
+…+ 
= 
，
设函数f（x）=x﹣ 
，（m≥3，m∈N*）．
当x∈（0，+∞）时，函数f（x）=x﹣ 为单调增函数．
∵当t∈N*，∴1＜ 
≤2．∴f（ ）≤2﹣ 
．
即 c1+c2+…+cm≤2﹣ ．
【解析】（1）利用等差数列的定义及其性质即可得出；（2）设等差数列b1 ， b2 ， …，bm的公差为d．由b1= ，可得b2≤ ，再利用等差数列的通项公式及其不等式的性质即可证明；（3）设c1= （t∈N*），等比数列c1 ， c2 ， …，cm的公比为q．由c2≤ ，可得q= ≤ ．从而cn=c1qn﹣1≤ （1≤n≤m，n∈N*）．再利用等比数列的前n项和公式、函数的单调性即可得出．
【考点精析】通过灵活运用数列的前n项和和等差数列的性质，掌握数列{an}的前n项和sn与通项an的关系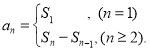
；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列即可以解答此题．
