题目内容
【题目】已知f(x)=﹣ex+ex(e为自然对数的底数)
(1)求函数f(x)的最大值;
(2)设g(x)=lnx+ ![]() x2+ax,若对任意x1∈(0,2],总存在x2∈(0,2].使得g(x1)<f(x2),求实数a的取值范围.
x2+ax,若对任意x1∈(0,2],总存在x2∈(0,2].使得g(x1)<f(x2),求实数a的取值范围.
【答案】
(1)解:f(x)=﹣ex+ex的导数为f′(x)=﹣ex+e,
当x∈(﹣∞,1)时,f′(x)>0,f(x)单调递增;
当x∈(1,+∞)时,f′(x)<0,f(x)单调递减;
故f(x)max=f(1)=0;
(2)解:对任意x1∈(0,2],总存在x2∈(0,2],
使得g(x1)<f(x2)等价于g(x1)<f(x2)max.
由(1)可知f(x2)max=f(1)=0.
问题转化为g(x)<0在x∈(0,2]恒成立.
参变量分离得:﹣a> ![]() =
= ![]() +
+ ![]() x,
x,
令r(x)= ![]() +
+ ![]() x,x∈(0,2],
x,x∈(0,2],
r′(x)= ![]() +
+ ![]() ,由0<x≤2时,1﹣lnx>0,得r′(x)>0,
,由0<x≤2时,1﹣lnx>0,得r′(x)>0,
即r(x)在x1∈(0,2]上单增.
故﹣a>r(x)max=r(2)= ![]() +1.
+1.
综上:a<﹣ ![]() ﹣1,
﹣1,
即a的取值范围为 (﹣∞,﹣ ![]() ﹣1).
﹣1).
【解析】(1)求得f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间,进而得到函数f(x)的最大值;(2)由题意可得g(x1)<f(x2)max . 由(Ⅰ)可得问题转化为g(x)<0在x∈(0,2]恒成立.运用参数分离,求得不等式右边函数的最大值,即可得到所求a的范围.

 名校课堂系列答案
名校课堂系列答案【题目】在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生

表二:女生

(1)从表二的非优秀学生中随机抽取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下面的![]() 列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.

参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中,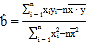 ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.