题目内容
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,该椭圆中心到直线
,该椭圆中心到直线![]() 的距离为
的距离为![]() .
.
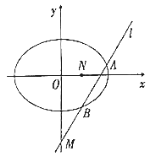
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() ,使直线
,使直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过定点
为直径的圆过定点![]() ?若存在,求出所有符合条件的直线方程;若不存在,请说明理由.
?若存在,求出所有符合条件的直线方程;若不存在,请说明理由.
【答案】(1) ![]() .
.
(2) 存在直线![]() :
:![]() 或
或![]() :
:![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
【解析】分析:由![]() ,该椭圆中心到直线
,该椭圆中心到直线![]() 的距离为
的距离为![]() ,
,![]() 求出椭圆方程;
求出椭圆方程;
(2)先假设存在这样的直线,设出直线方程(注意考虑斜率),与椭圆联立,考虑![]() 然后设
然后设![]() ,
,![]() ,利用韦达定理,利用
,利用韦达定理,利用![]() 为直径的圆过定点
为直径的圆过定点![]() ,转化
,转化![]() ,转化坐标构造方程进行求解。
,转化坐标构造方程进行求解。
详解:(1)直线![]() 的一般方程为
的一般方程为![]() ,
,
依题意得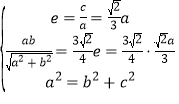 ,解得
,解得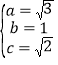 ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 即为
即为![]() 轴,此时
轴,此时![]() ,
,![]() 为椭圆
为椭圆![]() 的短轴端点,以
的短轴端点,以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
当直线![]() 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为![]() ,由
,由![]() ,
,
得![]() .
.
所以![]() ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则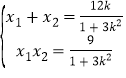 ,①
,①
而![]()
![]() .
.
因为以![]() 为直径的圆过定点
为直径的圆过定点![]() ,所以
,所以![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() .②
.②
将①式代入②式整理解得![]() .
.
综上可知,存在直线![]() :
:![]() 或
或![]() :
:![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
点晴:本题考查直线与椭圆的位置关系,这类题目一般涉及设直线方程,然后和椭圆联立,设点,考虑![]() ,然后利用韦达定理,接下来就是对题干的转化啦,本题中典型的垂直问题,主要转化方向就是向量点乘,因为斜率的话还需要考虑斜率是否存在。
,然后利用韦达定理,接下来就是对题干的转化啦,本题中典型的垂直问题,主要转化方向就是向量点乘,因为斜率的话还需要考虑斜率是否存在。

练习册系列答案
相关题目
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
