题目内容
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列和期望E(X).
【答案】(1)![]() ;(2)分布列见解析,期望为16.
;(2)分布列见解析,期望为16.
【解析】试题分析:
(1)利用对立事件公式可得该顾客中奖的概率为![]() ;
;
(2)由超几何分布求得分布列,然后求解数学期望可得期望值为16.
试题解析:
解法一:(1)P=I-![]() =1-
=1-![]() =
=![]() ,即该顾客中奖的概率为
,即该顾客中奖的概率为![]() .
.
(2)ξ的所有可能值为:0,10,20,50,60(元).P(ξ=0)=![]() =
=![]() ,P(ξ=10)=
,P(ξ=10)=![]() =
=![]() ,
,
P(ξ=20)=![]() =
=![]() ,P(ξ=50)=
,P(ξ=50)=![]() =
=![]() ,P(ξ=60)=
,P(ξ=60)=![]() =
=![]() .
.
ξ | 0 | 10 | 20 | 50 | 60 |
P |
|
|
|
| bn= 8an+1an-16an+1+2an+5=0, |
故ξ有分布列:
从而期望Eξ=0×![]() +10×
+10×![]() +20×
+20×![]() +50×
+50×![]() +60×
+60×![]() =16.
=16.
解法二:(1)P=![]() =
=![]() =
=![]() ,
,
(2)ξ的分布列求法同解法一
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值Eξ=2×8=16(元).

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中,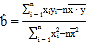 ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.