题目内容
若α+β=
，
（1）求（1-tanα）（1-tanβ）的值；
（2）求
的值．
| 3π |
| 4 |
（1）求（1-tanα）（1-tanβ）的值；
（2）求
| tan20°+tan40°+tan120° |
| tan20°tan40° |
考点：两角和与差的正切函数,三角函数的化简求值
专题：三角函数的求值
分析：根据正切函数的和差公式计算即可
解答：
解：（1）∵tan（α+β）=
=tan
=-1
∴（1-tanαtanβ）=-（tanα+tanβ）
∴（1-tanα）（1-tanβ）=1+tanαtanβ-（tanα+tanβ）=1+tanαtanβ+（1-tanαtanβ）=2，
（2）∵tan120°=-tan60°=-tan（20°+40°）=-
=-
，
∴tan20°+tan40°=
（1-tan20°tan40°）=
-
tan20°tan40°
∴
=
=-
| tanα+tanβ |
| 1-tanαtanβ |
| 3π |
| 4 |
∴（1-tanαtanβ）=-（tanα+tanβ）
∴（1-tanα）（1-tanβ）=1+tanαtanβ-（tanα+tanβ）=1+tanαtanβ+（1-tanαtanβ）=2，
（2）∵tan120°=-tan60°=-tan（20°+40°）=-
| tan20°+tan40° |
| 1-tan20°tan40° |
| 3 |
∴tan20°+tan40°=
| 3 |
| 3 |
| 3 |
∴
| tan20°+tan40°+tan120° |
| tan20°tan40° |
| ||||||
| tan20°tan40° |
| 3 |
点评：本题考查了正切函数的两角的和差公式的应用，关键是灵活变形，属于基础题
练习册系列答案
相关题目
要得到函数y=cos（2x-
）的图象，只需将函数y=cos（2x+
）的图象（ ）
| 2π |
| 3 |
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
若两个非零向量
、
，互相垂直，则下列一定成立的是（ ）
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、(
|
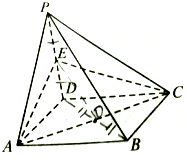如图，四棱锥P-ABCD的侧面PAD是正三角形，且垂直于底面，底面ABCD是矩形，E是PD的中点，求证：平面ACE⊥平面PCD．{an}为等比数列，Sn是其前n项和，若a2•a3=8a1，且a4与2a5的等差中项为20，则S5=（ ）
| A、29 | B、30 | C、31 | D、32 |