题目内容
若函数y=f（x）在[-2，2]是奇函数，且在[0，2]上最大值是5，则函数f（x）在[-2，0]上的最小值是 ．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：先根据奇函数的对称特征，判断函数在区间[-2，0]上的最小值情况．
解答：
解：∵奇函数f（x），
∴其图象关于原点对称，
又f（x）在[0，2]上最大值是5，
由对称性知：
函数f（x）在[-2，0]上的最小值：-5．
故答案为：-5．
∴其图象关于原点对称，
又f（x）在[0，2]上最大值是5，
由对称性知：
函数f（x）在[-2，0]上的最小值：-5．
故答案为：-5．
点评：本小题主要考查函数单调性的应用、函数奇偶性的应用、函数的最值及其几何意义、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
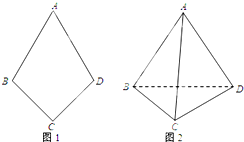如图1，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=
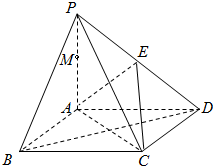如图，棱锥P-ABCD的底面ABCD是矩形，PA⊥面ABCD，PA=AD=4，BD=4