题目内容
附加题（10分，总分120以上有效）
（1）设函数f（x）=（x-3）3+x-1，{an}是公差不为0的等差数列，f（a1）+f（a2）+…+f（a7）=14，则a1+a2+…+a7=______
（2）若Sn=sin
+sin
+…+sin
（n∈N+），则在S1，S2，…S100中，正数的个数是______．
（1）设函数f（x）=（x-3）3+x-1，{an}是公差不为0的等差数列，f（a1）+f（a2）+…+f（a7）=14，则a1+a2+…+a7=______
（2）若Sn=sin
| π |
| 7 |
| 2π |
| 7 |
| nπ |
| 7 |
（1）∵f（x）=（x-3）3+x-1，∴f（x）-2=（x-3）3+x-3，
令g（x）=f（x）-2，
∴g（x）关于（3，0）对称，
∵f（a1）+f（a2）+…+f（a7）=14，
∴f（a1）-2+f（a2）-2+…+f（a7）-2=0
∴g（a1）+g（a2）+…+g（a7）=0，
∴g（a4）为g（x）与x轴的交点，
因为g（x）关于（3，0）对称，所以a4=3，
∴a1+a2+…+a7=7a4=21，
故答案为：21．
（2）∵sin
＞0，sin
＞0，…，sin
＞0，sin
=0，sin
＜0，…，sin
＜0，sin
=0，
∴S1=sin
＞0，
S2=sin
+sin
＞0，…，
S8=sin
+sin
+…+sin
+sin
+sin
=sin
+…+sin
+sin
＞0，
…，
S12＞0，
而S13=sin
+sin
+…+sin
+sin
+sin
+sin
+…+sin
=0，
S14=S13+sin
=0+0=0，
又S15=S14+sin
=0+sin
=S1＞0，S16=S2＞0，…S27=S13=0，S28=S14=0，
∴S14n-1=0，S14n=0（n∈N*），在1，2，…100中，能被14整除的共7项，
∴在S1，S2，…，S100中，为0的项共有14项，其余项都为正数．
故在S1，S2，…，S100中，正数的个数是86．
故答案为：86．
令g（x）=f（x）-2，
∴g（x）关于（3，0）对称，
∵f（a1）+f（a2）+…+f（a7）=14，
∴f（a1）-2+f（a2）-2+…+f（a7）-2=0
∴g（a1）+g（a2）+…+g（a7）=0，
∴g（a4）为g（x）与x轴的交点，
因为g（x）关于（3，0）对称，所以a4=3，
∴a1+a2+…+a7=7a4=21，
故答案为：21．
（2）∵sin
| π |
| 7 |
| 2π |
| 7 |
| 6π |
| 7 |
| 7π |
| 7 |
| 8π |
| 7 |
| 13π |
| 7 |
| 14π |
| 7 |
∴S1=sin
| π |
| 7 |
S2=sin
| π |
| 7 |
| 2π |
| 7 |
S8=sin
| π |
| 7 |
| 2π |
| 7 |
| 6π |
| 7 |
| 7π |
| 7 |
| 8π |
| 7 |
| 2π |
| 7 |
| 6π |
| 7 |
| 7π |
| 7 |
…，
S12＞0，
而S13=sin
| π |
| 7 |
| 2π |
| 7 |
| 6π |
| 7 |
| 7π |
| 7 |
| 8π |
| 7 |
| 9π |
| 7 |
| 13π |
| 7 |
S14=S13+sin
| 14π |
| 7 |
又S15=S14+sin
| 15π |
| 7 |
| π |
| 7 |
∴S14n-1=0，S14n=0（n∈N*），在1，2，…100中，能被14整除的共7项，
∴在S1，S2，…，S100中，为0的项共有14项，其余项都为正数．
故在S1，S2，…，S100中，正数的个数是86．
故答案为：86．
练习册系列答案
相关题目
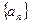中，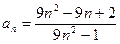
.
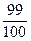是否为该数列的项，为什么？
； 
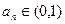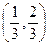内有无数列的项，若有，有几项？若无，说明理由.
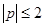的所有实数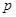
，求使不等式
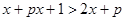恒成立的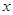
取值范围.
，
，那么
是这个数列的第 项.