题目内容
14.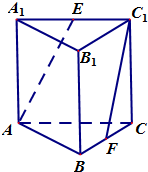 如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(1)求证:直线AB⊥平面BCC1B1;
(2)求异面直线AE与C1F所成的角的正弦值.
分析 (1)根据三棱柱ABC-A1B1C1中,侧棱垂直于底面,得到侧棱BB1与AB垂直,再由AB⊥BC,且BC∩BB1=B,即可得证;
(2)如图,取AC的中点G,连结C1F,GF,易得AE∥C1G,确定出∠GC1F就是异面直线AE与C1F所成的角,求出即可.
解答 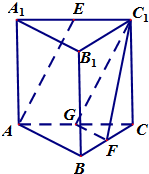 (1)证明:在三棱柱ABC,A1B1C1中,BB1⊥底面ABC,
(1)证明:在三棱柱ABC,A1B1C1中,BB1⊥底面ABC,
∴BB1⊥AB,
又∵AB⊥BC,BC∩BB1=B,
∴AB⊥平面B1BCC1;
(2)解:如图,取AC的中点G,连结C1F,GF,易得AE∥C1G,
∴∠GC1F就是异面直线AE与C1F所成的角,
由(1)可知直线AB⊥平面BCC1B1,
∴AB⊥C1F,
又AB∥GF,
∴GF⊥C1F,
在Rt△ABC中,根据勾股定理得:AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{3}$,
∴GF=$\frac{\sqrt{3}}{2}$,
又在Rt△CC1G中,根据勾股定理得:C1G=$\sqrt{C{G}^{2}+C{{C}_{1}}^{2}}$=$\sqrt{5}$,
∴sin∠GC1F=$\frac{GF}{{C}_{1}G}$=$\frac{\sqrt{15}}{10}$,
则异面直线AE与C1F所成的角的正弦值为$\frac{{\sqrt{15}}}{10}$.
点评 此题考查了异面直线及其所成的角,平面与平面垂直的判定,确定出异面直线所求的角是解本题的关键.

练习册系列答案
相关题目
4.下列函数中,是偶函数的是( )
| A. | f(x)=x2 | B. | f(x)=2x | C. | f(x)=x3 | D. | f(x)=$\frac{1}{x}$ |
2.设集合A={x|x=π+$\frac{2kπ}{3}$,k∈z},B={x|x=kπ+$\frac{π}{3}$,k∈z},C={x|x=kπ+$\frac{2π}{3}$,k∈z},则A∩(B∪C)=( )
| A. | $\left\{{x|x=kπ+\frac{π}{3},k∈z}\right\}$ | B. | $\left\{{x|x=kπ-\frac{π}{3},k∈z}\right\}$ | C. | $\left\{{x|x=2kπ±\frac{π}{3},k∈z}\right\}$ | D. | $\left\{{x|x=kπ±\frac{π}{3},k∈z}\right\}$ |
9.复数z=$\frac{1-i}{2+i}$(i为虚数单位)的虚部为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$i |
6.已知A,B均为锐角,sinA=$\frac{{\sqrt{5}}}{5}$,sinB=$\frac{{\sqrt{10}}}{10}$,则A+B的值为( )
| A. | $\frac{7π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
4.点M的极坐标是$(2,\frac{2π}{3})$,则点M直角坐标是( )
| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{3},1)$ | C. | $(-1,\sqrt{3})$ | D. | $(\sqrt{3},-1)$ |