题目内容
4.点M的极坐标是$(2,\frac{2π}{3})$,则点M直角坐标是( )| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{3},1)$ | C. | $(-1,\sqrt{3})$ | D. | $(\sqrt{3},-1)$ |
分析 利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,可求出点的直角坐标.
解答 解:x=ρcosθ=2×cos$\frac{2π}{3}$=-1,
y=ρsinθ=2×sin$\frac{2π}{3}$=$\sqrt{3}$,
∴将极坐标(2,$\frac{2π}{3}$)化为直角坐标是(-1,$\sqrt{3}$).
故选:C.
点评 本题主要考查了点的极坐标和直角坐标的互化,同时考查了三角函数求值,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13.在下列向量组中,能作为向量基底的是( )
| A. | $\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(2,3)$ | B. | $\overrightarrow{e_1}=(-1,3),\overrightarrow{e_2}=(5,-2)$ | ||
| C. | $\overrightarrow{e_1}=(3,4),\overrightarrow{e_2}=(6,8)$ | D. | $\overrightarrow{e_1}=(2,-3),\overrightarrow{e_2}=(-2,3)$ |
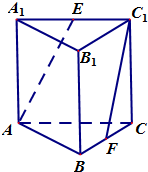 如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.