题目内容
6.已知A,B均为锐角,sinA=$\frac{{\sqrt{5}}}{5}$,sinB=$\frac{{\sqrt{10}}}{10}$,则A+B的值为( )| A. | $\frac{7π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
分析 由条件利用同角三角函数的基本关系,求得cosA 和cosB的值,可得cos(A+B)=cosAcosB-sinAsinB 的值,再根据A+B的范围,求得A+B的值.
解答 解:∵A,B均为锐角,sinA=$\frac{{\sqrt{5}}}{5}$,sinB=$\frac{{\sqrt{10}}}{10}$,
∴cosA=$\sqrt{{1-sin}^{2}A}$=$\frac{2\sqrt{5}}{5}$,cosB=$\sqrt{{1-sin}^{2}B}$=$\frac{3\sqrt{10}}{10}$,A+B∈(0,π).
再根据cos(A+B)=cosAcosB-sinAsinB=$\frac{2\sqrt{5}}{5}×\frac{3\sqrt{10}}{10}$-$\frac{\sqrt{5}}{5}×\frac{\sqrt{10}}{10}$=$\frac{\sqrt{2}}{2}$,
∴A+B=$\frac{π}{4}$,
故选:D.
点评 本题主要考查同角三角函数的基本关系,两角和的余弦公式,属于基础题.

练习册系列答案
相关题目
11.下列结构图中,框①、②处理该分别填入( )


| A. | l?α,l⊥α | B. | l?α,l与α相交 | C. | l?α,l⊥α | D. | l?α,l与α相交 |
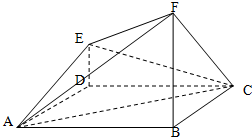 一个多面体如图所示,四边形ABCD是边长为2的正方形,AB=FB,FB⊥平面ABCD,ED∥FB,且ED=1.
一个多面体如图所示,四边形ABCD是边长为2的正方形,AB=FB,FB⊥平面ABCD,ED∥FB,且ED=1.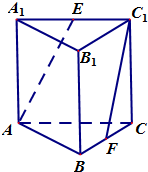 如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.