题目内容
19.计算是积分${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=π.分析 ${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx表示以原点为圆心,2为半径的圆面积的$\frac{1}{4}$,问题得以解决.
解答 解:令y=$\sqrt{4-{x}^{2}}$,则x2+y2=4(y≥0),点(x,y)的轨迹表示半圆,
${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx表示以原点为圆心,2为半径的圆面积的$\frac{1}{4}$,
故${∫}_{0}^{2}$$\sqrt{4-{x}^{2}}$dx=$\frac{1}{4}$π×4=π,
故答案为:π.
点评 本题考查定积分的几何意义,属基础题

练习册系列答案
相关题目
7.2014年世界经济形势严峻,某企业为了增强自身竞争力,计划对职工进行技术培训,以提高产品的质量.为了解某车间对技术培训的态度与性别的关系,对该车间所有职工进行了问卷调查得到了如下的2×2列联表:
(1)用分层抽样的方法在不赞成的职工中抽5人进行调查,其中男职工、女职工各抽取多少人?
(2)在上述抽取的5人中选2人,求至少有一名男职工的概率;
(3)据此资料,判断对技术培训的态度是否与性别有关?并证明你的结论.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
| 赞成 | 不赞成 | 合计 | |
| 男职工 | 22 | 8 | 30 |
| 女职工 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
(2)在上述抽取的5人中选2人,求至少有一名男职工的概率;
(3)据此资料,判断对技术培训的态度是否与性别有关?并证明你的结论.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
4.已知曲线y=$\frac{{x}^{2}}{4}$-3lnx+1的一条切线的斜率为$\frac{1}{2}$,则切点的横坐标为( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
11.下列结构图中,框①、②处理该分别填入( )


| A. | l?α,l⊥α | B. | l?α,l与α相交 | C. | l?α,l⊥α | D. | l?α,l与α相交 |
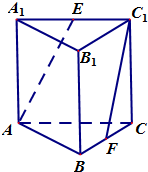 如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点. 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2.
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2.