题目内容
4．下列函数中，是偶函数的是（ ）| A． | f（x）=x2 | B． | f（x）=2x | C． | f（x）=x3 | D． | f（x）=$\frac{1}{x}$ |
分析 运用奇偶性的定义，逐一判断各个选项中的函数的奇偶性，从而得出结论．
解答 解：由于函数f（x）=x2的定义域为R，且有f（-x）=（-x）2=x2=f（x），
是偶函数，故A满足条件；
由于函数f（x）=2x是指数函数，不具奇偶性，是非奇非偶函数，故排除B；
由于函数f（x）=x3的定义域为R，且有f（-x）=（-x）3=-x3=-f（x），
是奇函数，故排除C；
由于函数f（x）=$\frac{1}{x}$的定义域为{x|x≠0}，且f（-x）=$\frac{1}{-x}$=-$\frac{1}{x}$=-f（x）是奇函数，故排除D．
故选A．
点评 本题主要考查函数的奇偶性的判断，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
15．为了研究某灌溉渠道水的流速y与水深x之间的关系，测得一组数据如下表：
（1）画出散点图，判断变量y与x是否具有相关关系；
（2）若y与x之间具有线性相关关系，求y对x的回归直线方程； （$\sum_{i=1}^5{x_i^2}=16.3$，$\sum_{i=1}^5{{x_i}{y_i}}=18.5$）
（3）预测水深为1.95m水的流速是多少．
参考公式：$b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$．
| 水深x（m） | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 流速y（m/s） | 1 | 1.5 | 2 | 2.5 | 3 |
（2）若y与x之间具有线性相关关系，求y对x的回归直线方程； （$\sum_{i=1}^5{x_i^2}=16.3$，$\sum_{i=1}^5{{x_i}{y_i}}=18.5$）
（3）预测水深为1.95m水的流速是多少．
参考公式：$b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$．
如图，已知梯形ABCD中，AB∥DC，且AB=2CD，E、F分别是DC、AB的中点，设$\overrightarrow{AD}=\overrightarrow a，\overrightarrow{AB}=\overrightarrow b$，试用$\overrightarrow a$、$\overrightarrow b$为基底表示$\overrightarrow{BC}$、$\overrightarrow{EF}$．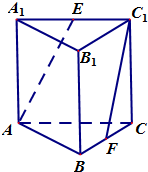
如图所示，在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1=AC=2，BC=1，E，F分别是A1C1，BC的中点．