题目内容
已知数列{an}是等差数列,且a1=1,a1+a2+a3=6.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=an2n.求数列{bn}前n项和的公式.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=an2n.求数列{bn}前n项和的公式.
(Ⅰ)设公差为d,
∵a1+a2+a3=6.a1=1,
∴3a1+3d=6,解得d=1,
∴数列{an}的通项公式an=n.
(Ⅱ)∵an=n,bn=an2n.
∴bn=an2n=n•2n,
则Sn=1×2+2×22+3×23+???+n?2n ①
2Sn=1×22+2×23+…+(n-1)×2n+n×2n+1,②
①式减去②式,得(1-2)Sn=(2+22+…2n)-n×2n+1=
-n×2n+1,
∴Sn=2n+1(n-1)+2.
∵a1+a2+a3=6.a1=1,
∴3a1+3d=6,解得d=1,
∴数列{an}的通项公式an=n.
(Ⅱ)∵an=n,bn=an2n.
∴bn=an2n=n•2n,
则Sn=1×2+2×22+3×23+???+n?2n ①
2Sn=1×22+2×23+…+(n-1)×2n+n×2n+1,②
①式减去②式,得(1-2)Sn=(2+22+…2n)-n×2n+1=
| 2×(1-2n) |
| 1-2 |
∴Sn=2n+1(n-1)+2.

练习册系列答案
相关题目
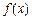 定义如下表,数列
定义如下表,数列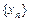 满足
满足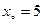 且
且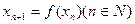 ,则
,则 .
.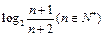 ,前n项和为Sn,则使Sn<-5成立的自然数n有
,前n项和为Sn,则使Sn<-5成立的自然数n有