题目内容
设数列{an}是公差大于零的等差数列,已知a1=2,a3=a22-10.
(1)求{an}的通项公式;
(2)设数列{bn}是以函数f(x)=4sin2πx的最小正周期为首项,以3为公比的等比数列,求数列{an•bn}的前n项和Sn.
(1)求{an}的通项公式;
(2)设数列{bn}是以函数f(x)=4sin2πx的最小正周期为首项,以3为公比的等比数列,求数列{an•bn}的前n项和Sn.
(1)设{an}的公差为d,d>0,
∵a1=2,a3=a22-10,
∴
,解得a=2或d=-4(舍).(5分)
∴an=2+(n-1)×2=2n.(6分)
(2)∵y=4sin2πx=4×
=-2cos2πx+2,
其最小正周期为
=1,
∴首项为b1=1.(7分)
∵公比为q=3,从而bn=3n-1,
∴an•bn=2n•3n-1,(8分)
∴Sn=2•30+4•3+6•32+…+2n•3n-1,①
3Sn=2•3+4•32+6•33+…+2n•3n,②
①-②,得:-2Sn=2+2(3+32+33+…+3n-1)-2n•3n
=2+2×
-2n•3n
=2+3n-3-2n•3n,
∴Sn=
.(12分)
∵a1=2,a3=a22-10,
∴
|
∴an=2+(n-1)×2=2n.(6分)
(2)∵y=4sin2πx=4×
| 1-cos2πx |
| 2 |
=-2cos2πx+2,
其最小正周期为
| 2π |
| 2π |
∴首项为b1=1.(7分)
∵公比为q=3,从而bn=3n-1,
∴an•bn=2n•3n-1,(8分)
∴Sn=2•30+4•3+6•32+…+2n•3n-1,①
3Sn=2•3+4•32+6•33+…+2n•3n,②
①-②,得:-2Sn=2+2(3+32+33+…+3n-1)-2n•3n
=2+2×
| 3(1-3n-1) |
| 1-3 |
=2+3n-3-2n•3n,
∴Sn=
| (2n-1)•3n+1 |
| 2 |

练习册系列答案
相关题目
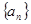 ,定义
,定义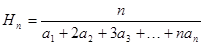 为
为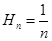 ,则数列
,则数列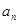 = .
= .