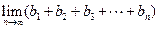题目内容
设an(n=2,3,4…)是(3+
)n展开式中x的一次项的系数,则
(
+
+…+
)的值是______.
| x |
| 2010 |
| 2009 |
| 32 |
| a2 |
| 33 |
| a3 |
| 32010 |
| a2010 |
(3+
)n展开式的通项为
3n-r•(
)r=
x
,令
=1,得r=2.展开式中x的一次项的系数为3n-2Cn2,即an=3n-2Cn2 (n≥2).
我∴
=
=
=18(
-
),,∴
(
+
+…+
)=
×18×(1-
+
-
+…
-
)=18×
×(1-
)=18×1=18
故答案为:18.
| x |
| C | rn |
| x |
| 3n-rC | rn |
| r |
| 2 |
| r |
| 2 |
我∴
| 3n |
| an |
| 32 | ||
|
| 18 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
| 2010 |
| 2009 |
| 32 |
| a2 |
| 33 |
| a3 |
| 32010 |
| a2010 |
| 2010 |
| 2009 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2009 |
| 1 |
| 2010 |
| 2010 |
| 2009 |
| 1 |
| 2010 |
故答案为:18.

练习册系列答案
相关题目
 ,且
,且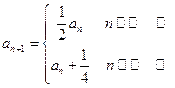 ,
,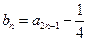 ,n==l,2,3,…·.
,n==l,2,3,…·.