题目内容
数列{an}的通项公式为an=(-1)n-1(4n-3),则S100等于______.
由题意可得:数列{an}的通项公式为an=(-1)n-1•(4n-3),
所以a1=1,a2=-5,a3=9,a4=-13,…a99=393,a100=-397,
所以S100=(a1+a2)+(a3+a4)+…+(a99+a100),
所以S100=-(4+4+…+4)=-200.
故答案为:-200.
所以a1=1,a2=-5,a3=9,a4=-13,…a99=393,a100=-397,
所以S100=(a1+a2)+(a3+a4)+…+(a99+a100),
所以S100=-(4+4+…+4)=-200.
故答案为:-200.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,
, ,当
,当 时,
时, 等于
等于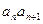 的个位数,若数列
的个位数,若数列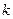 项和为243,则
项和为243,则 中,
中, ,则数列
,则数列 项的绝对值之和为( )
项的绝对值之和为( )