题目内容
3.设函数y=|ex-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x1、x2(x1<x2),与直线y=m的两交点横坐标分别为x3、x4(x3<x4),若m∈(0,$\frac{1}{2}$),则(x4+x1)-(x3+x2)的取值范围是( )| A. | (-∞,0) | B. | (-∞,ln$\frac{3}{5}$) | C. | (ln$\frac{3}{5}$,0) | D. | (-∞,-1) |
分析 由条件求得x1,x2,x3,x4,得到(x4+x1)-(x3+x2)=ln$\frac{{m}^{2}+m}{2-m-{m}^{2}}$,令t=ln$\frac{{m}^{2}+m}{2-m-{m}^{2}}$,则原式=lnt,利用不等式的基本性质求得$\frac{1}{t}$的范围,可得t的范围,从而求得lnt的范围,即为所求
解答 解:由方程|ex-1|=$\frac{1}{m+1}$的两根为x1,x2(x1<x2),
求得x1=ln$\frac{m}{m+1}$,x2=ln$\frac{m+2}{m+1}$.
由方程|ex-1|=m的两根为x3,x4(x3<x4),
求得x3=ln(1-m),x4=ln(1+m).
∴(x4+x1)-(x3+x2)=lnm-ln$\frac{(2+m)(1-m)}{m+1}$=ln$\frac{{m}^{2}+m}{2-m-{m}^{2}}$.
令t=ln$\frac{{m}^{2}+m}{2-m-{m}^{2}}$,则原式=lnt,且$\frac{1}{t}$=-1+$\frac{2}{{m}^{2}+m}$=-1+$\frac{2}{(m+\frac{1}{2})^{2}-\frac{1}{4}}$.
由m∈(0,$\frac{1}{2}$),可得 0<$(m+\frac{1}{2})^{2}-\frac{1}{4}$<$\frac{3}{4}$,$\frac{2}{(m+\frac{1}{2})^{2}-\frac{1}{4}}$>$\frac{8}{3}$,
∴$\frac{1}{t}$=-1+$\frac{2}{(m+\frac{1}{2})^{2}-\frac{1}{4}}$>$\frac{5}{3}$,则0<t<$\frac{3}{5}$.
故原式=lnt∈(-∞,ln$\frac{3}{5}$),
故选:B.
点评 本题主要考查指数函数的综合应用,不等式的基本性质,二次函数的性质,体现了转化的数学思想,属于中档题.

| A. | [5,11] | B. | [4,11] | C. | [4,12] | D. | [4,15] |
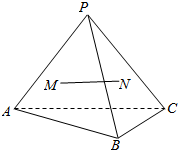 在三棱锥P-ABC中,M,N是△PAB与△PBC的重心,求证:MN∥平面ABC.
在三棱锥P-ABC中,M,N是△PAB与△PBC的重心,求证:MN∥平面ABC.