题目内容
14.若C${\;}_{21}^{k-4}$<C${\;}_{21}^{k-2}$<C${\;}_{21}^{k-1}$(k∈N),则k的取值范围是( )| A. | [5,11] | B. | [4,11] | C. | [4,12] | D. | [4,15] |
分析 直接利用组合数公式化简不等式求解即可.
解答 解:C${\;}_{21}^{k-4}$<C${\;}_{21}^{k-2}$<C${\;}_{21}^{k-1}$(k∈N),
可得$\frac{21!}{(k-4)!(25-k)!}<\frac{21!}{(k-2)!(23-k)!}<\frac{21!}{(k-1)!(22-k)!}$,k-4≥0,
即$\frac{1}{(25-k)(24-k)}<\frac{1}{(k-2)(k-3)}$并且$\frac{1}{23-k}<\frac{1}{k-1}$,
解得:4≤k<12.
k的取值范围是[4,11].
故选:B.
点评 本题考查组合数公式的应用,不等式组的解法,考查计算能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
4.已知$\overrightarrow{m}$=(sin(2α+β),cosβ),$\overrightarrow{n}$=(cos(2α-β),sinβ),且$\overrightarrow{m}$∥$\overrightarrow{n}$,则锐角α,β的值为( )
| A. | α=$\frac{π}{4}$,β任意 | B. | α任意,β=$\frac{π}{4}$ | C. | α=β=$\frac{π}{4}$ | D. | α任意,β任意 |
3.设函数y=|ex-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x1、x2(x1<x2),与直线y=m的两交点横坐标分别为x3、x4(x3<x4),若m∈(0,$\frac{1}{2}$),则(x4+x1)-(x3+x2)的取值范围是( )
| A. | (-∞,0) | B. | (-∞,ln$\frac{3}{5}$) | C. | (ln$\frac{3}{5}$,0) | D. | (-∞,-1) |
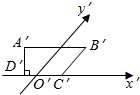 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积. 在一次青年歌手大奖赛中,七位评委为某参赛选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分,所剩数据的平均值为83.
在一次青年歌手大奖赛中,七位评委为某参赛选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分,所剩数据的平均值为83.