题目内容
15.化简:$\frac{1}{2!}$+$\frac{2}{3!}$+$\frac{3}{4!}$+…+$\frac{n-1}{n!}$.(n∈N*,n≥2)分析 原式利用题中的新定义变形,找出规律,以此类推得到结果即可.
解答 解:$\frac{1}{2!}$+$\frac{2}{3!}$+$\frac{3}{4!}$+…+$\frac{n-1}{n!}$
=$\frac{2!-1}{2!}$+$\frac{2}{3!}$+$\frac{3}{4!}$+…+$\frac{n-1}{n!}$
=1-$\frac{1}{2!}$+$\frac{2}{3!}$+$\frac{3}{4!}$+…+$\frac{n-1}{n!}$
=1-$\frac{1}{3!}$+$\frac{3}{4!}$+…+$\frac{n-1}{n!}$
=1-$\frac{1}{n!}$
故答案为:1-$\frac{1}{n!}$.
点评 此题考查了排列数公式的应用,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
3.设函数y=|ex-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x1、x2(x1<x2),与直线y=m的两交点横坐标分别为x3、x4(x3<x4),若m∈(0,$\frac{1}{2}$),则(x4+x1)-(x3+x2)的取值范围是( )
| A. | (-∞,0) | B. | (-∞,ln$\frac{3}{5}$) | C. | (ln$\frac{3}{5}$,0) | D. | (-∞,-1) |
20.若$\sqrt{4{a}^{2}-4a+1}$=$\root{3}{(1-2a)^{3}}$,则实数a的取值范围是( )
| A. | a∈R | B. | a=$\frac{1}{2}$ | C. | a>$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
15.已知函数g(x)=sinx+acosx+2017满足g(x)+g($\frac{7π}{3}$-x)=4034,又f(x)=asinx+cosx对任意x恒有f(x)≤|f(x0)|,则满足条件的x0可以是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{5π}{6}$ | D. | 以上选项均不对 |
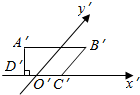 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.