题目内容
11．
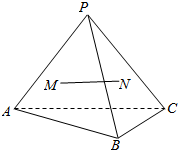在三棱锥P-ABC中，M，N是△PAB与△PBC的重心，求证：MN∥平面ABC．
分析 连接PM，PN分别与AB，BC交于D，E，则D，E是AB，BC的中点，利用M、N分别是△PAB、△PBC的重心，可得DE∥MN，根据直线与平面平行的判定定理可得结论．
解答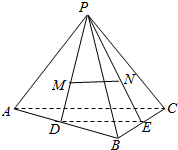 
证明：连接PM，PN分别与AB，BC交于D，E，则D，E是AB，BC的中点，
∵M、N分别是△PAB、△PBC的重心，
∴DE∥MN，
∵MN?平面ABC，DE?平面ABC，
∴MN∥平面ABC．
点评 本题考查直线与平面平行的判定，考查学生分析解决问题的能力和推来论证能力，属于基本知识的考查．
练习册系列答案
寒假学与练系列答案
相关题目
在一次青年歌手大奖赛中，七位评委为某参赛选手打出的分数的茎叶图如图所示，去掉一个最高分和一个最低分，所剩数据的平均值为83．
3．设函数y=|ex-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x1、x2（x1＜x2），与直线y=m的两交点横坐标分别为x3、x4（x3＜x4），若m∈（0，$\frac{1}{2}$），则（x4+x1）-（x3+x2）的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，ln$\frac{3}{5}$） | C． | （ln$\frac{3}{5}$，0） | D． | （-∞，-1） |
20．若$\sqrt{4{a}^{2}-4a+1}$=$\root{3}{（1-2a）^{3}}$，则实数a的取值范围是（ ）
| A． | a∈R | B． | a=$\frac{1}{2}$ | C． | a＞$\frac{1}{2}$ | D． | a≤$\frac{1}{2}$ |