题目内容
13.求函数y=$\frac{{x}^{2}-2x+3}{{x}^{2}-x+2}$的值域.分析 可将原函数整理成关于x的方程的形式:(y-1)x2+(2-y)x+2y-3=0,方程有解,可讨论y=1和y≠1:y=1时,容易判断出满足方程有解;而y≠1时,方程为一元二次方程,方程有解,便有△≥0,这样解不等式即可得出原函数的值域.
解答 解:由原函数得:yx2-yx+2y=x2-2x+3,整理得:
(y-1)x2+(2-y)x+2y-3=0,看成关于x的方程,方程有解;
①若y=1,则x-1=0,满足方程有解;
②若y≠1,则△=(2-y)2-4(y-1)(2y-3)≥0;
解得$\frac{8-2\sqrt{2}}{7}≤y≤\frac{8+2\sqrt{2}}{7}$;
∴原函数的值域为:[$\frac{8-2\sqrt{2}}{7},\frac{8+2\sqrt{2}}{7}$].
点评 考查函数值域的概念,形如$y=\frac{a{x}^{2}+bx+c}{d{x}^{2}+ex+f}$的函数的值域求法:整理成关于x的方程,根据方程有解求,一元二次方程有解时判别式△的取值情况.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
3.5个人排队,其中甲、乙、丙3人按甲、乙、丙的顺序排队的方法有( )
| A. | 12 | B. | 20 | C. | 16 | D. | 120 |
4.已知$\overrightarrow{m}$=(sin(2α+β),cosβ),$\overrightarrow{n}$=(cos(2α-β),sinβ),且$\overrightarrow{m}$∥$\overrightarrow{n}$,则锐角α,β的值为( )
| A. | α=$\frac{π}{4}$,β任意 | B. | α任意,β=$\frac{π}{4}$ | C. | α=β=$\frac{π}{4}$ | D. | α任意,β任意 |
3.设函数y=|ex-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x1、x2(x1<x2),与直线y=m的两交点横坐标分别为x3、x4(x3<x4),若m∈(0,$\frac{1}{2}$),则(x4+x1)-(x3+x2)的取值范围是( )
| A. | (-∞,0) | B. | (-∞,ln$\frac{3}{5}$) | C. | (ln$\frac{3}{5}$,0) | D. | (-∞,-1) |
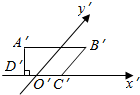 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.