Question

18．在四面体S-ABCD中，底面为矩形，SA⊥平面ABCD，M，N分别为AB，SC的中点．
（1）求证：MN⊥CD；
（2）若∠SDA=45°，求证：MN⊥平面SCD．

Answer 1

分析 （1）取SD中点E，连接AE，NE，可证MN∥AE，由SA⊥CD，AD⊥CD，AD∩AS=A，可证CD⊥平面SAD，从而可证CD⊥AE，即可证明MN⊥CD．
（2）先证明AE⊥SD，由（1）可得AE⊥CD，CD∩SD=D，即可证明AE⊥平面SDC，由MN∥AE，即可得证．

解答 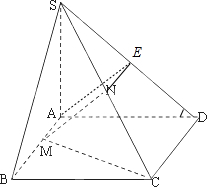证明：（1）取SD中点E，连接AE，NE，
则NE=$\frac{1}{2}$CD=AM，NE∥CD∥AM，
∴四边形AMNE为平行四边形，
∴MN∥AE，
∵SA⊥平面ABCD，CD?平面ABCD，
∴SA⊥CD，
∵底面为矩形，AD⊥CD，AD∩AS=A，
∴CD⊥平面SAD，
∵AE?平面SAD，
∴CD⊥AE，
∴由MN∥AE，可得MN⊥CD．
（2）∵SA⊥平面ABCD，∠SDA=45°，
∴SA=AD，E为SD中点，
∴AE⊥SD，
∵由（1）可得AE⊥CD，CD∩SD=D，
∴AE⊥平面SDC，
∵MN∥AE，可得MN⊥平面SCD．

点评 本题考查的知识点是直线与平面垂直的判定，空间中直线与直线之间的位置关系，其中熟练掌握空间直线与平面平行、垂直、夹角的定义、判定、性质是解答本题的关键，属于中档题．