题目内容
2. 如图,平面α∥平面β,点A,C∈α,B,D∈β,点E,F分别在线段AB,CD上,且$\frac{AE}{EB}$=$\frac{CF}{FD}$,求证:EF∥β.
如图,平面α∥平面β,点A,C∈α,B,D∈β,点E,F分别在线段AB,CD上,且$\frac{AE}{EB}$=$\frac{CF}{FD}$,求证:EF∥β.
分析 过点C作CM∥AB,交平面β于点M,在平面ACMB中,过点E作EN∥BM,交CM于点N,
证明平面EFN∥β,即可证明EF∥β.
解答 证明:如图所示,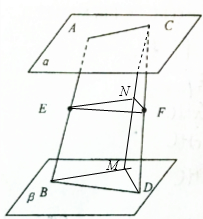
过点C作CM∥AB,交平面β于点M,
连接BM,在平面ACMB中,过点E作EN∥BM,交CM于点N,
连接FN,
∵EN∥BM,∴$\frac{AE}{EB}$=$\frac{CN}{NM}$,
又∵$\frac{AE}{EB}$=$\frac{CF}{FD}$,
∴$\frac{CN}{NM}$=$\frac{CF}{FD}$,
∴NF∥MD;
且BM?β,EN?β,
∴EN∥β,
同理NF∥β;
又EN∩NF=N,EN?平面EFN,NF?平面EFN,
∴平面EFN∥β;
又EF?平面EFN,
∴EF∥β.
点评 本题考查了空间中的平行关系的应用问题,也考查了空间想象能力与逻辑思维能力的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.在三棱锥S-ABC中,AB⊥BC,AB=BC=$\sqrt{2}$,SA=SC=2.AC的中点为M,∠SMB的余弦值为$\frac{\sqrt{3}}{3}$,若S、A、B、C都在同一球面上,则该球的表面积为( )
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
11.如果a<3,则下列结论一定正确的是( )
| A. | a2>9 | B. | a2<9 | C. | a3>27 | D. | a3<27 |
12.下列点在曲线$\left\{\begin{array}{l}x={sin^2}θ\\ y=cosθ\end{array}\right.$上的是( )
| A. | (2,1) | B. | (-3,-2) | C. | $({\frac{3}{4},-\frac{1}{2}})$ | D. | (1,1) |
 如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,试建立适当的坐标系,求截口BAC所在椭圆的方程.
如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,试建立适当的坐标系,求截口BAC所在椭圆的方程. 已知⊙O1的半径为R,周长为C.
已知⊙O1的半径为R,周长为C.