题目内容
9. 如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,试建立适当的坐标系,求截口BAC所在椭圆的方程.
如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,试建立适当的坐标系,求截口BAC所在椭圆的方程.
分析 以F1F2的中点为坐标原点,以F1F2为x轴建立平面直角坐标系,设截口BAC所在椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,根据已知及椭圆的性质,求出a,b,可得答案.
解答 解:建立如图所示的平面直角坐标系,设截口BAC所在椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,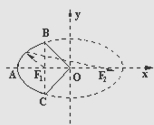
因为BC⊥F1F2,|F1B|=3m,|F1F2|=4cm,
所以在直角△BF1F2中,
|BF2|=4=$\sqrt{{{BF}_{1}}^{2}+{F}_{1}{{F}_{2}}^{2}}$=5cm,
故2a=|F1B|+|BF2|=8cm,a=4cm,
2c=|F1F2|=4cm,c=2cm,
又由b2=a2-c2=12,
故截口BAC所在椭圆的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$
点评 本题考查的知识点是椭圆的标准方程,椭圆的应用,建立恰当的坐标系是解答的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
19.棱长为2的正方体的顶点都在同一个球面上,则该球的体积和表面积分别是( )
| A. | $2\sqrt{3}π,12π$ | B. | $4\sqrt{3}π,12π$ | C. | $2\sqrt{3}π,6π$ | D. | $4\sqrt{3}π,6π$ |
20.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到我市周一至周五某一时间段车流量与PM2.5的数据如表
(Ⅰ)根据表中数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(Ⅱ)规定当一天内PM2.5的浓度平均值在(0,35]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(35,75]内,空气质量等级为良.为使我国某日空气质量等级为优或良,则应控制当天车流量在多少万辆以内?(结果保留整数)
附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 59 | 55 | 52 | 51 | 58 |
| PM2.5的浓度平均值y(微克/立方米) | 81 | 67 | 66 | 59 | 77 |
(Ⅱ)规定当一天内PM2.5的浓度平均值在(0,35]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(35,75]内,空气质量等级为良.为使我国某日空气质量等级为优或良,则应控制当天车流量在多少万辆以内?(结果保留整数)
附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
4.设t是函数f(x)=ex+lnx的零点,若x0>t,则f(x0)的值满足( )
| A. | f(x0)=0 | B. | f(x0)>0 | C. | f(x0)<0 | D. | f(x0)的符号不确定 |
14.设α∈(-$\frac{π}{2}$,0),cosα=$\frac{1}{2}$,则tan(α+$\frac{π}{6}$)=( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
18. 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为( )
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为( )
 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为( )
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为( )| A. | 32 | B. | 48+16$\sqrt{2}$ | C. | 64 | D. | 32+16$\sqrt{2}$ |
 如图,平面α∥平面β,点A,C∈α,B,D∈β,点E,F分别在线段AB,CD上,且$\frac{AE}{EB}$=$\frac{CF}{FD}$,求证:EF∥β.
如图,平面α∥平面β,点A,C∈α,B,D∈β,点E,F分别在线段AB,CD上,且$\frac{AE}{EB}$=$\frac{CF}{FD}$,求证:EF∥β.