题目内容
10. 已知⊙O1的半径为R,周长为C.
已知⊙O1的半径为R,周长为C.(1)在⊙O1内任意作三条弦,其长分别是l1、l2、l3.求证:l1+l2+l3<C;
(2)如图,在直角坐标系xOy中,设⊙O1的圆心为O1(R,R).
①当直线l:y=x+b(b>0)与⊙O1相切时,求b的值;
②当反比例函数y=$\frac{k}{x}$(k>0)的图象与⊙O1有两个交点时,求k的取值范围.
分析 (1)根据圆的任意一条弦都小于或等于圆的直径解答;
(2)①设直线与圆相切于点M,连接O1M,则O1M⊥l,过点O1作直线NH⊥x轴,与l交于点N,与x轴交于点H,因为直线的k=1,所以直线与x轴的夹角等于45°,△OMN是等腰直角三角形,点N的坐标即可表示出来,再把点N的坐标代入直线解析式,即可求出b值;
②利用反比例函数图象关于直线y=x对称,作直线y=x的图象与圆有两交点,根据直线与x轴的夹角是45°,用圆的半径表示出两个交点坐标,分别代入反比例函数表达式求出k的值,k的取值就在这两个数值之间.
解答 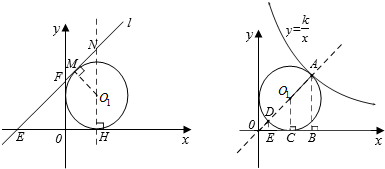 (1)证明:∵l1≤2R,l2≤2R,l3≤2R.
(1)证明:∵l1≤2R,l2≤2R,l3≤2R.
∴l1+l2+l3≤3×2R<π×2R=C,
因此,l1+l2+l3<C.
(2)解:①如图,根据题意可知⊙O1与x轴、y轴分别相切,
设直线l与⊙O1相切于点M,则O1M⊥l,
过点O1作直线NH⊥x轴,与l交于点N,
与x轴交于点H,
又∵直线l与x轴、y轴分别交于
点E(-b,0)、F(0,b),
∴OE=OF=b,∴∠NEO=45°,
∴∠ENO1=45°,
在Rt△O1MN中,O1N=O1M÷sin45°=$\sqrt{2}R$,
∴点N的坐标为N(R,$\sqrt{2}R+R$),
把点N坐标代入y=x+b得:$\sqrt{2}R+R=R+b$,
解得:$b=\sqrt{2}R$;
②如图,设经过点O、O1的直线交⊙O1于点A、D,
由已知,直线OO1:y=x是圆与反比例函数图象的对称轴,
当反比例函数$y=\frac{k}{x}$的图象与⊙O1直径AD相交时(点A、D除外),
则反比例函数$y=\frac{k}{x}$的图象与⊙O1有两个交点.
过点A作AB⊥x轴交x轴于点B,
过O1作O1C⊥x轴于点C,OO1=O1C÷sin45°=$\sqrt{2}R$,OA=$\sqrt{2}R+R$,
所以OB=AB=OA•sin45°=$(\sqrt{2}R+R)•\frac{{\sqrt{2}}}{2}$=$R+\frac{{\sqrt{2}}}{2}R$,
因此点A的坐标是A$(R+\frac{{\sqrt{2}}}{2}R,R+\frac{{\sqrt{2}}}{2}R)$,将点A的坐标 代入$y=\frac{k}{x}$,
解得:$k=(\frac{3}{2}+\sqrt{2}){R^2}$.
同理可求得点D的坐标为D$(R-\frac{{\sqrt{2}}}{2}R,R-\frac{{\sqrt{2}}}{2}R)$,
将点D的坐标代入$y=\frac{k}{x}$,解得:$k=(\frac{3}{2}-\sqrt{2}){R^2}$
所以当反比例函数$y=\frac{k}{x}(k>0)$的图象与⊙O1有两个交点时,
k的取值范围是:$(\frac{3}{2}-\sqrt{2}){R^2}<k<(\frac{3}{2}+\sqrt{2}){R^2}$
点评 本题考查:(1)直径是圆中最长的弦,其它任意弦都小于或等于圆的直径;
(2)一次函数图象的性质和反比例函数图象的性质,结合圆的特点直线的k等于1时与x轴的夹角等于45°是解本题的关键,也是解决本题的突破口.

 金钥匙试卷系列答案
金钥匙试卷系列答案| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 59 | 55 | 52 | 51 | 58 |
| PM2.5的浓度平均值y(微克/立方米) | 81 | 67 | 66 | 59 | 77 |
(Ⅱ)规定当一天内PM2.5的浓度平均值在(0,35]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(35,75]内,空气质量等级为良.为使我国某日空气质量等级为优或良,则应控制当天车流量在多少万辆以内?(结果保留整数)
附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
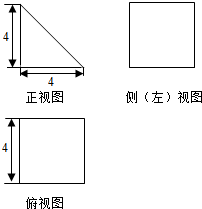 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为( )
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为( )| A. | 32 | B. | 48+16$\sqrt{2}$ | C. | 64 | D. | 32+16$\sqrt{2}$ |
| A. | $\frac{{4\sqrt{2}}}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $4\sqrt{2}$ |
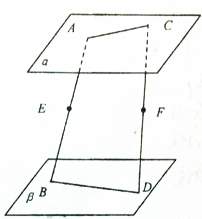 如图,平面α∥平面β,点A,C∈α,B,D∈β,点E,F分别在线段AB,CD上,且$\frac{AE}{EB}$=$\frac{CF}{FD}$,求证:EF∥β.
如图,平面α∥平面β,点A,C∈α,B,D∈β,点E,F分别在线段AB,CD上,且$\frac{AE}{EB}$=$\frac{CF}{FD}$,求证:EF∥β.