题目内容
8.已知二次函数f(x)=ax2-4bx+1(a≠0).(1)若a=1,b∈[-1,1],求函数y=f(x)在[1,+∞)上是增函数的概率;
(2)设(a,b)是区域$\left\{\begin{array}{l}x+y-8≤0\\ x>0\\ y>0\end{array}\right.$,内的随机点,求函数y=f(x)在[1,+∞)上的增函数的概率.
分析 (1)求出函数y=f(x)在[1,+∞)上是增函数的b 的范围,利用区域长度比求概率;
(2)画出区域,求出满足条件的区域面积,利用面积比求概率.
解答 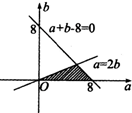 解:函数y=f(x)在[1,+∞)上是增函数,则a>0且$\frac{2b}{a}≤1$,即a>0且a≥2b;
解:函数y=f(x)在[1,+∞)上是增函数,则a>0且$\frac{2b}{a}≤1$,即a>0且a≥2b;
(1)因为a=1,则$b≤\frac{1}{2}$时,函数f(x)为增函数
所以函数y=f(x)在[1,+∞)上是增函数的概率$p=\frac{{\frac{1}{2}-({-1})}}{{1-({-1})}}=\frac{3}{4}$;
(2)由(1)知当且仅当a≥2b,且a>0时,函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
依条件可知实验的全部结果所构成的区域为不等式组所表示的平面区域.
构成所求事件的区域为图中的阴影部分.
由$\left\{\begin{array}{l}a+b-8=0\\ b=\frac{a}{2}\end{array}\right.$,得交点的坐标为$({\frac{16}{3},\frac{8}{3}})$,故所求事件的概率为$p=\frac{{\frac{1}{2}×8×\frac{8}{3}}}{{\frac{1}{2}×8×8}}=\frac{1}{3}$.
点评 本题考查了几何概型公式的运用;关键是明确满足条件的a,b的范围,找出集合测度(区域长度,面积或者体积),利用概率公式解答.

练习册系列答案
相关题目
18.复数$\frac{5i}{1-2i}$的共轭复数是( )
| A. | -2+i | B. | -2-i | C. | 2+i | D. | 2-i |
19.若复数$\frac{a+i}{2i}$的实部和虚部相等,则实数a=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
16.已知点A(0,2),抛物线C:y2=ax,(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,若|FM|:|MN|=1:$\sqrt{5}$,则a的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
3.已知奇函数f(x)的定义域为(2a,a+1),求f(a+$\frac{1}{3}$)的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
20.若等轴双曲线经过点(2,1),则该双曲线的实轴长是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
17.某环保部门对甲、乙两类A型品牌车各抽取5辆进行CO2排放量检测,记录如下(单位:g/km).
经测算发现,乙品牌车CO2排放量的平均值为$\overline{{x}_{乙}}$=120g/km.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO2排放量超过130(g/km)的概率是多少?
(Ⅱ)若90<x<130,试比较甲、乙两类品牌车CO2排放量的稳定性.
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | y | 160 |
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO2排放量超过130(g/km)的概率是多少?
(Ⅱ)若90<x<130,试比较甲、乙两类品牌车CO2排放量的稳定性.
18.已知等差数列{an}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=( )
| A. | 123 | B. | 105 | C. | 95 | D. | 23 |