题目内容
20.若等轴双曲线经过点(2,1),则该双曲线的实轴长是( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 设等轴双曲线的方程为x2-y2=λ≠0.把点(2,1),代入解得λ,进而根据双曲线的性质可得双曲线的实轴长.
解答 解:设等轴双曲线的方程为x2-y2=λ≠0.
把点(2,1)代入可得:4-1=λ,解得λ=3.
∴等轴双曲线的方程为x2-y2=3.
即双曲线的标准方程为$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{3}=1$,
故a=$\sqrt{3}$,2a=$2\sqrt{3}$,
即双曲线的实轴长为$2\sqrt{3}$,
故选:A.
点评 本题考查的知识点是双曲线的标准方程和简单性质,熟练掌握等轴双曲线的标准方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.对任意正数x,y,不等式$\frac{x}{3x+y}+\frac{3y}{x+3y}≤k$恒成立,则实数k的取值范围是( )
| A. | $[{\frac{5}{4},+∞})$ | B. | $[{\frac{{6-\sqrt{3}}}{4},+∞})$ | C. | [1,+∞) | D. | $[{\frac{{\sqrt{3}}}{2},+∞})$ |
15.设集合A={x|x2≤x},B={x|$\frac{1}{x}$≥1},则A∩B=( )
| A. | (-∞,1] | B. | [0,1] | C. | (0,1] | D. | (-∞,0)∪(0,1] |
5.双曲线$\frac{x^2}{{{m^2}-4}}+\frac{y^2}{m^2}$=1(m∈Z)的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
12.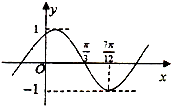 已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
 已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )| A. | 向右平移 $\frac{π}{6}$个长度单位 | B. | 向右平移 $\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移 $\frac{π}{12}$个长度单位 |