题目内容
13.△ABC中,内角A,B,C的对边分别为a,b,c,且满足(2c-a)cosB-bcosA=0(Ⅰ)若b=7,a+c=13,求△ABC的面积;
(Ⅱ)求${sin^2}A+sin(C-\frac{π}{6})$的取值范围.
分析 (Ⅰ)利用正弦定理把已知等式中的边转化为角的正弦,整理求得cosB,进而求得B.
(Ⅱ)把${sin^2}A+sin(C-\frac{π}{6})$转化为cosA的解析式,进而根据cosA的范围确定答案.
解答 解:(Ⅰ)∵(2c-a)cosB-bcosA=0,
由正弦定理得(2sinC-sinA)cosB-sinBcosA=0,
则2sinCcosB-sin(A+B)=0,
求得cosB=$\frac{1}{2}$,B=$\frac{π}{3}$.
由余弦定理得b2=a2+c2-2accosB,
即49=(a+c)2-2ac-2accosB,求得ac=40,
∴三角形△ABC面积S=$\frac{1}{2}$acsinB=10$\sqrt{3}$.
(Ⅱ)${sin^2}A+sin(C-\frac{π}{6})$=sin2A+sin($\frac{2π}{3}$-A-$\frac{π}{6}$)=sin2A+sin($\frac{π}{2}$-A)=-cos2A+cosA+1,A∈(0,$\frac{2π}{3}$),
令u=cosA∈(-$\frac{1}{2}$,1)
y=-u2+u+1∈($\frac{1}{4}$,$\frac{5}{4}$].
点评 本题主要考查了余弦定理和增弦定理的应用.解题的关键是利用正弦定理和余弦定理对边角问题进行转化.

练习册系列答案
相关题目
3.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=$\frac{x}{2}$+y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
4.对于函数f(x)=eax-lnx,(a是实常数),下列结论正确的一个是( )
| A. | a=1时,B有极大值,且极大值点(1,3) | |
| B. | a=2时,A有极小值,且极小值点x0∈(0,$\frac{1}{4}$) | |
| C. | a=$\frac{1}{2}$时,D有极小值,且极小值点x0∈(1,2) | |
| D. | a<0时,C有极大值,且极大值点x0∈(-∞,0) |
1.已知i是虚数单位,则复数z=i2015的虚部是( )
| A. | 0 | B. | -1 | C. | 1 | D. | -i |
5.双曲线$\frac{x^2}{{{m^2}-4}}+\frac{y^2}{m^2}$=1(m∈Z)的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
3.某人最近7天收到的聊天信息数分别是5,10,6,8,9,7,11,则该组数据的方差为( )
| A. | $\frac{24}{7}$ | B. | 4 | C. | $\frac{16}{7}$ | D. | 3 |
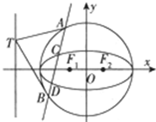 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.