题目内容
16．已知点A（0，2），抛物线C：y2=ax，（a＞0）的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，若|FM|：|MN|=1：$\sqrt{5}$，则a的值等于（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 4 |
分析 作出M在准线上的射影，根据|KM|：|MN|确定|KN|：|KM|的值，进而列方程求得a．
解答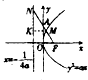 
解：抛物线C：y2=ax，（a＞0）的焦点$F（\frac{a}{4}，0）$，
设M在准线上的射影为K，
由抛物线的定义知|MF|=|MK|，
∴|KM|：|MN|=1：$\sqrt{5}$，
则|KN|：|KM|=2：1，
∴kFN=$\frac{0-2}{\frac{a}{4}-0}$=-$\frac{2}{\frac{a}{4}}$=-2，
∴a=4．
故选：D．
点评 本题主要考查了抛物线的简单性质．抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
7．P是双曲线$\frac{x^2}{4}$-y2=1右支（在第一象限内）上的任意一点，A1，A2分别是左右顶点，O是坐标原点，直线PA1，PO，PA2的斜率分别为k1，k2，k3，则斜率之积k1k2k3的取值范围是（ ）
| A． | （0，1） | B． | （0，$\frac{1}{8}$） | C． | （0，$\frac{1}{4}$） | D． | （0，$\frac{1}{2}$） |
4．对于函数f（x）=eax-lnx，（a是实常数），下列结论正确的一个是（ ）
| A． | a=1时，B有极大值，且极大值点（1，3） | |
| B． | a=2时，A有极小值，且极小值点x0∈（0，$\frac{1}{4}$） | |
| C． | a=$\frac{1}{2}$时，D有极小值，且极小值点x0∈（1，2） | |
| D． | a＜0时，C有极大值，且极大值点x0∈（-∞，0） |
1．已知i是虚数单位，则复数z=i2015的虚部是（ ）
| A． | 0 | B． | -1 | C． | 1 | D． | -i |
5．双曲线$\frac{x^2}{{{m^2}-4}}+\frac{y^2}{m^2}$=1（m∈Z）的离心率为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{5}$ | D． | 3 |
6．设椭圆$\frac{x^2}{m^2}+\frac{y^2}{{{m^2}-1}}$=1（m＞1）上一点到其左焦点的距离为3，到右焦点的距离为1，则椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{3}{4}$ |