题目内容
14.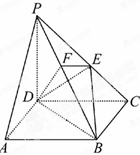 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
分析 (1)先证明线线平行,从而得到线面平行;(2)根据线面垂直的判定定理进行证明即可.
解答 证明:(1)连结AC,设AC∩BD=O,连接EO,
∵底面是正方形,∴O为AC的中点,OE为△PAC的中位线,
∴PA∥OE,而OE?平面EDB,PA?平面EBD,
∴PA∥平面EDB;
(2)∵PD⊥平面AC,BC?平面AC,
∴BC⊥PD,而BC⊥CD,PD∩CD=D,
∴BC⊥平面PDC,
∵DE?平面AC,∴BC⊥DE,①,
又∵PD⊥平面AC,DC?平面AC,
∴PD⊥DC,而PD=DC,
∴△PDC为等腰三角形,∴DE⊥PC,②,
由①②得:DE⊥平面PBC,
∴DE⊥PB,又EF⊥PB,
∴PB⊥平面DEF.
点评 本题考查了线面平行,线面垂直的判定定理,熟练掌握判定定理是解题的关键,本题是一道中档题.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
5.等差数列{an}中,a5=3,a17=2a8
(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n+1}}{a_n}}}(n∈{N^*})$,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n+1}}{a_n}}}(n∈{N^*})$,求数列{bn}的前n项和Sn.
17.一个几何体的三视图如图所示,则该几何体的体积是( )
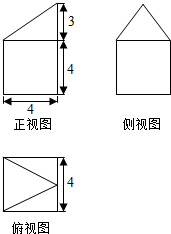

| A. | 64 | B. | 72 | C. | 80 | D. | 112 |