题目内容
19.如图,在棱长均为1的直三棱柱ABC-A1B1C1中,D是BC的中点.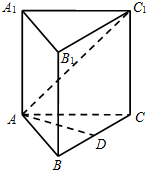
(1)求证:AD⊥平面BCC1B1;
(2)求直线AC1与面BCC1B1所成角的正弦值.
分析 (1)直三棱柱的侧棱和底面垂直,从而可得到AD⊥BB1,并且AD⊥BC,从而由线面垂直的判定定理可得到AD⊥平面BCC1B1;
(2)连接C1D,从而可得到∠AC1D为直线AC1和平面BCC1B1所成角,在Rt△AC1D中,容易求出AD,AC1,从而sin∠AC1D=$\frac{AD}{A{C}_{1}}$.
解答 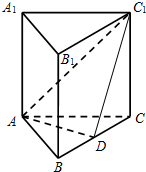 证:(1)直三棱柱ABC-A1B1C1中,BB1⊥面ABC;
证:(1)直三棱柱ABC-A1B1C1中,BB1⊥面ABC;
∴BB1⊥AD,又∵AB=AC,D是BC的中点;
∴AD⊥BC,BC∩BB1=B;
∴AD⊥平面BCC1B1;
(2)连接C1D,由(1)AD⊥平面BCC1B1;
则∠AC1D即为直线AC1与面BCC1B1所成角;
在直角△AC1D中,$AD=\frac{{\sqrt{3}}}{2}$,$A{C_1}=\sqrt{2}$,$sin∠A{C_1}D=\frac{AD}{{A{C_1}}}=\frac{{\sqrt{6}}}{4}$;
即直线AC1与面BCB1C1所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.
点评 考查直三棱柱的定义,线面垂直的性质,线面垂直的判定定理,以及线面角的定义,正弦函数的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知直线过点A(m,m),B(m-1,m+1),则直线AB的倾斜角为( )
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | 以m的值有关 |
7.下列四个函数中,以π为最小正周期,且在区间($\frac{π}{2}$,π)上为减函数的是( )
| A. | y=cosx | B. | y=|2sinx| | C. | y=cos$\frac{x}{2}$ | D. | y=tanx |
2.等差数列{an}中,a1>0,d<0,S3=S11,则Sn中的最大值是( )
| A. | S7 | B. | S7或S8 | C. | S14 | D. | S8 |
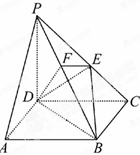 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.