题目内容
4.函数y=asinx+bcosx(x∈R)的最大值是3.则a2+b2的值为9.分析 由条件利用辅助角公式化简函数的解析式,再利用正弦函数的值域求得a2+b2的值.
解答 解:函数y=asinx+bcosx=$\sqrt{{a}^{2}{+b}^{2}}$($\frac{a}{\sqrt{{a}^{2}{+b}^{2}}}$sinx+$\frac{b}{\sqrt{{a}^{2}{+b}^{2}}}$cosx),
令cosθ=$\frac{a}{\sqrt{{a}^{2}{+b}^{2}}}$,sinθ=$\frac{b}{\sqrt{{a}^{2}{+b}^{2}}}$,则函数y=$\sqrt{{a}^{2}{+b}^{2}}$ sin(x+θ),
故函数y的最大值为$\sqrt{{a}^{2}{+b}^{2}}$=3,则a2+b2的值为9,
故答案为:9.
点评 本题主要考查辅助角公式,正弦函数的值域,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.设a=$\int_{1}^{2}{(3{x^2}-2x)dx}$,则二项式${(a{x^2}-\frac{1}{x})^6}$的展开式中的常数项为( )
| A. | 120 | B. | -120 | C. | -240 | D. | 240 |
13.把一枚硬币任意抛掷三次,事件A表示“至少一次出现反面”,事件B表示“恰有一次出现正面”,则P(B|A)值等于( )
| A. | $\frac{21}{64}$ | B. | $\frac{7}{64}$ | C. | $\frac{1}{7}$ | D. | $\frac{3}{7}$ |
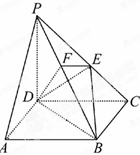 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.