题目内容
6.已知双曲线 C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,A B 为左、右顶点,点 P 为双曲线 C 在第一象限的任意一点,点 O 为坐标原点,若直线PA,PB,PO 的斜率分别为k1,k2,k3,记m=k1k2k3,则 m 的取值范围为(0,2$\sqrt{2}$).分析 由已知条件推导出b=$\sqrt{2}$a,k1k2=$\frac{y}{x+a}•\frac{y}{x-a}$=2,0<k3<$\sqrt{2}$,由此能求出m=k1k2k3的取值范围.
解答 解:∵双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,
∴e=$\frac{c}{a}$=$\sqrt{3}$,∴b=$\sqrt{2}$a,
设P(x,y),∵点P为双曲线C在第一象限的任意一点,∴$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
∵A,B为双曲线C的左右顶点,点O为坐标原点,PA,PB,PO的斜率为k1,k2,k3,
∴k1k2=$\frac{y}{x+a}•\frac{y}{x-a}$=2,
又∵双曲线渐近线为y=$±\sqrt{2}$x,∴0<k3<$\sqrt{2}$,
∴0<m=k1k2k3<2$\sqrt{2}$,
故答案为:(0,2$\sqrt{2}$).
点评 本题考查斜率乘积的取值范围的求法,是中档题,解题时要认真审题,要熟练掌握双曲线的简单性质.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.直线4kx-4y-k=0与抛物线y2=x交于A,B两点,若|AB|=4,则弦AB的中点到直线x=-$\frac{1}{2}$的距离等于( )
| A. | $\frac{7}{4}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
1.从6双不同颜色的手套中任取4只,其中恰好有两只颜色相同的取法有( )
| A. | 60 | B. | 120 | C. | 180 | D. | 240 |
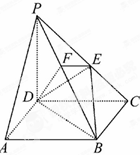 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.