题目内容
2.设函数f(x)=lnx-ax(a∈R).(1)若函数f(x)在x=2处的切线方程为y=x-b,求a,b的值;
(2)若函数g(x)=f(x)+$\frac{1}{2}$x2有两个极值点,且h(x)=ax-ex在(1,+∞)有最大值,求a的取值范围;
(3)讨论方程f(x)=0解的个数,并证明你的结论.
分析 (1)求出函数f(x)的导数,由题意可得f′(2)=1,f(2)=2-b,解方程可得a,b;
(2)求出g(x)的导数,由题意可得x2-ax+1=0有两个正根,则△=a2-4>0,且a>0,解得a>2,求得h(x)的导数,对a讨论,若2<a≤e,若a>e,判断h(x)的单调性,即可得到a的范围;
(3)方程f(x)=0即为a=$\frac{lnx}{x}$,令m(x)=$\frac{lnx}{x}$(x>0),求得导数,求出单调区间和最值,作出图象,通过图象对a讨论,即可得到解的个数.
解答 解:(1)函数f(x)=lnx-ax的导数f′(x)=$\frac{1}{x}$-a,
由函数f(x)在x=2处的切线方程为y=x-b,
可得f′(2)=1,f(2)=2-b,
即为$\frac{1}{2}$-a=1,ln2-2a=2-b,
解得a=-$\frac{1}{2}$,b=1-ln2;
(2)g(x)=lnx-ax+$\frac{1}{2}$x2的导数为g′(x)=$\frac{1}{x}$-a+x=$\frac{{x}^{2}-ax+1}{x}$
g(x)有两个极值点,即有x2-ax+1=0有两个正根,
则△=a2-4>0,且a>0,解得a>2,
h(x)=ax-ex的导数为h′(x)=a-ex,
若2<a≤e,h′(x)<0,h(x)在(1,+∞)单调递减,无最大值;
若a>e,则当1<x<lna,h′(x)>0,h(x)递增,当x>lna时,h′(x)<0,h(x)递减.
即有x=lna处取得最大值h(lna),
则有a>e成立;
(3)方程f(x)=0即为a=$\frac{lnx}{x}$,
由m(x)=$\frac{lnx}{x}$(x>0)的导数为m′(x)=$\frac{1-lnx}{{x}^{2}}$,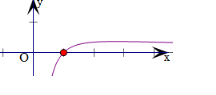
当x∈(0,e)时,m′(x)>0,m(x)递增,
当x∈(e,+∞)时,m′(x)<0,m(x)递减.
即有m(x)的最大值为m(e)=$\frac{1}{e}$,
y=m(x)的图象如右.
则当a>$\frac{1}{e}$时,y=a和y=m(x)无交点,即方程解的个数为0;
当0<a<$\frac{1}{e}$,y=a和y=m(x)有两个交点,即方程解的个数为2;
当a≤0时,y=a和y=m(x)有一个交点,即方程解的个数为1.
点评 本题考查导数的运用:求切线的斜率和单调区间和极值、最值,考查函数方程的转化思想的运用,运用分类讨论的思想方法是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 120 | B. | -120 | C. | -240 | D. | 240 |
| A. | $\frac{21}{64}$ | B. | $\frac{7}{64}$ | C. | $\frac{1}{7}$ | D. | $\frac{3}{7}$ |
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | 以m的值有关 |
| A. | $\frac{7}{4}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
| A. | y=cosx | B. | y=|2sinx| | C. | y=cos$\frac{x}{2}$ | D. | y=tanx |
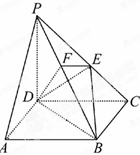 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.