题目内容
5.等差数列{an}中,a5=3,a17=2a8(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n+1}}{a_n}}}(n∈{N^*})$,求数列{bn}的前n项和Sn.
分析 (1)利用a17=2a8即3+12d=2(3+3d)可知公差d=$\frac{1}{2}$,进而计算即得结论;
(2)通过裂项可知bn=4($\frac{1}{n+1}$-$\frac{1}{n+2}$),并项相加即得结论.
解答 解:(1)设等差数列{an}的公差为d,
∵a5=3,
∴a8=a5+3d=3+3d,a17=a5+12d=3+12d,
又∵a17=2a8,即3+12d=2(3+3d),
∴d=$\frac{1}{2}$,
∴an=a5+(n-5)d=3+$\frac{n-5}{2}$=$\frac{n+1}{2}$;
(2)∵an=$\frac{n+1}{2}$,
∴bn=$\frac{1}{{a}_{n+1}{a}_{n}}$=$\frac{1}{\frac{n+1}{2}•\frac{n+2}{2}}$=4($\frac{1}{n+1}$-$\frac{1}{n+2}$),
∴Sn=4($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=4($\frac{1}{2}$-$\frac{1}{n+2}$)
=$\frac{2n}{n+2}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
13.把一枚硬币任意抛掷三次,事件A表示“至少一次出现反面”,事件B表示“恰有一次出现正面”,则P(B|A)值等于( )
| A. | $\frac{21}{64}$ | B. | $\frac{7}{64}$ | C. | $\frac{1}{7}$ | D. | $\frac{3}{7}$ |
10.已知直线过点A(m,m),B(m-1,m+1),则直线AB的倾斜角为( )
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | 以m的值有关 |
17.直线4kx-4y-k=0与抛物线y2=x交于A,B两点,若|AB|=4,则弦AB的中点到直线x=-$\frac{1}{2}$的距离等于( )
| A. | $\frac{7}{4}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | 4 |
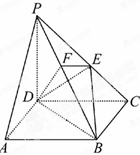 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.