题目内容
16.如果不论实数b取何值,直线y=kx+b与双曲线x2-2y2=1总有公共点,那么k的取值范围为-$\frac{\sqrt{2}}{2}$<k<$\frac{\sqrt{2}}{2}$.分析 将y=kx+b代入x2-2y2=1,得(1-2k2)x2-4kbx-2b2-1=0.(*),方程(*)对b∈R恒有解,可得△≥0,即可求得k的取值范围.
解答 解:将y=kx+b代入x2-2y2=1,得(1-2k2)x2-4kbx-2b2-1=0.(*)
当1-2k2=0即k=±$\frac{\sqrt{2}}{2}$时,4kbx+2b2+1=0不能使任意b∈R都有解.
∴1-2k2≠0.
∵方程(*)对b∈R恒有解,∴△≥0,
即16k2b2+4(1-2k2)(2b2-1)≥0恒成立,
即8k2≤8b2+4恒成立,
∴8k2≤4,∴k2≤$\frac{1}{2}$.
又k2≠$\frac{1}{2}$,∴k2<$\frac{1}{2}$,∴-$\frac{\sqrt{2}}{2}$<k<$\frac{\sqrt{2}}{2}$.
故答案为:-$\frac{\sqrt{2}}{2}$<k<$\frac{\sqrt{2}}{2}$.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,正确转化是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.把一枚硬币任意抛掷三次,事件A表示“至少一次出现反面”,事件B表示“恰有一次出现正面”,则P(B|A)值等于( )
| A. | $\frac{21}{64}$ | B. | $\frac{7}{64}$ | C. | $\frac{1}{7}$ | D. | $\frac{3}{7}$ |
11.在△ABC中,角A,B,C所对的边分别是a,b,c,若向量$\overrightarrow{p}$=(4,a2+b2-c2),$\overrightarrow{q}$=($\sqrt{3}$,$\frac{1}{2}$absinC),且满足$\overrightarrow{p}$∥$\overrightarrow{q}$,则C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
6.不等式x2-2x+1≥a2-2a对任意实数x恒成立,则实数a的取值范围为( )
| A. | (-∞,0]∪[2,+∞) | B. | (-∞,-2]∪[0,+∞) | C. | [0,2] | D. | [-2,0] |
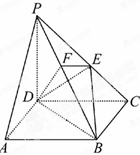 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.