题目内容
【题目】在平面直角坐标系xOy中，曲线C1的参数方程为
（φ为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2是圆心为（2，
），半径为1的圆．
（1）求曲线C1的普通方程和C2的直角坐标方程；
（2）设M为曲线C1上的点，N为曲线C2上的点，求|MN|的取值范围．
【答案】（1）C1：
y2＝1，C2 ：x2+（y﹣2）2＝1；（2）[0，
1]
【解析】
（Ⅰ）消去参数φ可得C1的直角坐标方程，易得曲线C2的圆心的直角坐标为（0，2），可得C2的直角坐标方程；（Ⅱ）设M（3cosφ，sinφ），由三角函数和二次函数可得|MC2|的取值范围，结合圆的知识可得答案．
（1）消去参数φ可得C1 的普通方程为
y2＝1，
∵曲线C2 是圆心为（2，
），半径为1 的圆，曲线C2 的圆心的直角坐标为（0，2），
∴C2 的直角坐标方程为x2+（y﹣2）2＝1；
（2）设M（3cosφ，sinφ），则|MC2|
，
∵﹣1≤sinφ≤1，∴1≤|MC2|
，
由题意结合图象可得|MN|的最小值为1﹣1＝0，最大值为
1，
∴|MN|的取值范围为[0，1]．
练习册系列答案
相关题目
【题目】某二手交易市场对某型号的二手汽车的使用年数
（
）与销售价格
（单位：万元/辆）进行整理，得到如下的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
（I）试求关于的回归直线方程
.
（参考公式：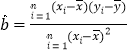
，
）
（II）已知每辆该型号汽车的收购价格为
万元，根据（I）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润
最大？（利润=销售价格-收购价格）
