题目内容
【题目】已知函数![]() .
.
(1)若![]() 时,函数
时,函数![]() 的图像恒在直线
的图像恒在直线![]() 上方,求实数
上方,求实数![]() 的取值范围;
的取值范围;
(2)证明:当时![]() ,
,![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先由题意得到当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立,再令
恒成立,再令![]() ,
,![]() ,用导函数方法研究其单调性,得到其最值,即可得出结果;
,用导函数方法研究其单调性,得到其最值,即可得出结果;
(2)根据数学归纳法的一般步骤,结合(1)的结果,即可证明结论成立.
(1)当![]() 时,函数
时,函数![]() 的图像恒在直线
的图像恒在直线![]() 上方,
上方,
等价于当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
令![]() ,
,![]() ,则
,则![]()
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上递增,
上递增,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上递减,
上递减,
∴![]() 为
为![]() 在区间
在区间![]() 上的极小值,仅有个极值点故为最小值,
上的极小值,仅有个极值点故为最小值,
∴![]() 时,
时,![]()
所以实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)证明:
①当![]() 时,由
时,由![]() ,知
,知![]() 成立;
成立;
②假设当![]() 时命题成立,即
时命题成立,即![]()
那么,当![]() 时,
时,![]()
![]()
下面利用分析法证明:![]()
要证上式成立,只需证:![]()
只需证:![]()
令![]() ,只需证:
,只需证:![]() ,
,![]()
只需证:![]() ,
,![]()
由(1)知当![]() 时,
时,![]() 恒成立.
恒成立.
所以,当![]() 时,
时,![]()
![]() 也成立,
也成立,
由①②可知,原不等式成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
运动达人 | 参与者 | 合计 | |
男教师 | 60 | 20 | 80 |
女教师 | 40 | 20 | 60 |
合计 | 100 | 40 | 140 |
(1)根据上表说明,能否在犯错误概率不超过0.05的前提下认为获得“运动达人”称号与性别有关?
(2)从具有“运动达人”称号的教师中,采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动,若从选取的10人中随机抽取3人作为代表参加开幕式,设抽取的3人中女教师人数为![]() ,写出
,写出![]() 的分布列并求出数学期望
的分布列并求出数学期望![]() .
.
参考公式: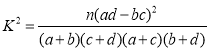 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
