题目内容
【题目】a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：
①当直线AB与a成60°角时，AB与b成30°角；
②当直线AB与a成60°角时，AB与b成60°角；
③直线AB与a所成角的最小值为45°；
④直线AB与a所成角的最大值为60°.
其中正确的是________.（填写所有正确结论的编号）
【答案】②③
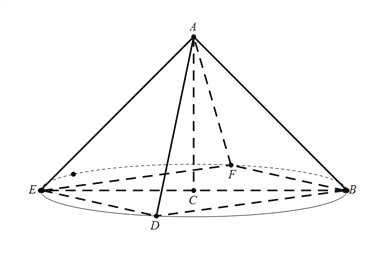
【解析】由题意，
是以AC为轴,BC为底面半径的圆锥的母线，由
，又AC⊥圆锥底面，所以在底面内可以过点B，作
，交底面圆
于点D，如图所示，连结DE，则DE⊥BD，
，连结AD，等腰
中，
,当直线AB与a成60°角时，
，故
，又在
中，
，过点B作BF∥DE，交圆C于点F，连结AF，由圆的对称性可知
,
为等边三角形，
，即AB与b成60°角，②正确，①错误.
由图可知③正确；很明显，可以满足平面ABC⊥直线a，则直线与
所成角的最大值为90°，④错误.
故正确的是②③.
练习册系列答案
相关题目
