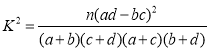题目内容
【题目】已知函数![]()
![]() .
.
(1)若曲线![]() 在
在![]() 处切线的斜率为
处切线的斜率为![]() ,求此切线方程;
,求此切线方程;
(2)若![]() 有两个极值点
有两个极值点![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.
【解析】分析:(1)由函数的解析式可得![]() ,利用
,利用![]() 可得
可得![]() , 则切点为
, 则切点为![]() ,切线方程为
,切线方程为![]() .
.
(2)结合(1)中导函数的解析令![]() ,得
,得![]() .构造函数,令
.构造函数,令![]() ,则
,则![]() ,利用导函数研究函数的单调性可知
,利用导函数研究函数的单调性可知![]() 在
在![]() 递增,在
递增,在![]() 递减,所以
递减,所以![]() . 结合题意可得
. 结合题意可得![]() 的取值范围是
的取值范围是![]() . 由极值点的性质可得
. 由极值点的性质可得![]() 不妨设
不妨设![]() ,则
,则![]() ,
,![]() ,结合
,结合![]() 的单调性可得
的单调性可得![]() ,据此有
,据此有![]() ,即
,即![]() .
.
详解:(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴![]() ,故切点为
,故切点为![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(2)![]() ,令
,令![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
令![]() ,得
,得![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 在
在![]() 递增,在
递增,在![]() 递减,所以
递减,所以![]() .
.
所以当![]() 时,
时,![]() 有一个极值点;
有一个极值点;
![]() 时,
时,![]() 有两个极值点;
有两个极值点;
当![]() 时,
时,![]() 没有极值点.
没有极值点.
综上,![]() 的取值范围是
的取值范围是![]() .
.
因为![]() 是
是![]() 的两个极值点,所以
的两个极值点,所以![]() 即
即![]() …①
…①
不妨设![]() ,则
,则![]() ,
,![]() ,
,
因为![]() 在
在![]() 递减,且
递减,且![]() ,所以
,所以![]() ,即
,即![]() …②.
…②.
由①可得![]() ,即
,即![]() ,
,
由①,②得![]() ,所以
,所以![]() .
.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.