题目内容
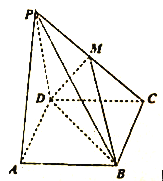
【题目】如图，隔河看两目标A、B，但不能到达，在岸边选取相距 
km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°（A、B、C、D在同一平面内），求两目标A、B之间的距离． 
【答案】解：在△ACD中，∠ADC=30°，∠ACD=120°，∴∠CAD=30°．
∴AC=CD= 
．
在△BDC中，∠CBD=180°﹣（45°+75°）=60°．
由正弦定理，得BC= 
．
由余弦定理，得AB2=AC2+BC2﹣2ACBCcos∠BCA
= 
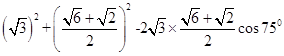=5．
∴AB= 
．
∴两目标A、B之间的距离为 km．
【解析】利用△ACD的边角关系得出AC，在△BCD中，由正弦定理即可得出BC，在△ACB中利用余弦定理即可得出AB．
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点，需要掌握正弦定理:
；余弦定理:
;
;
才能正确解答此题．
练习册系列答案
相关题目
