题目内容
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先求函数导数,转化为研究导函数零点,即方程![]() =0的根的情况,当
=0的根的情况,当![]() ,导函数不变号,在
,导函数不变号,在![]() 上单调递减,当
上单调递减,当![]() 时,有两个不等根,列表分析导函数符号变化规律,确定对应单调区间,(2)(i)利用导数几何意义化简条件:
时,有两个不等根,列表分析导函数符号变化规律,确定对应单调区间,(2)(i)利用导数几何意义化简条件: ![]() 在
在![]() ,
, ![]() 处的切线相互垂直,得
处的切线相互垂直,得![]() ,利用基本不等式证明不等式,(ii)先分别求出切线方程,再根据切线重合得
,利用基本不等式证明不等式,(ii)先分别求出切线方程,再根据切线重合得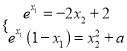 ,消元
,消元![]() 得
得![]() ,利用导数研究函数
,利用导数研究函数![]() ,
, ![]() 单调性,确定函数
单调性,确定函数![]() 值域,进而确定
值域,进而确定![]() 的取值范围.
的取值范围.
试题解析:解:(1)![]() ,则
,则![]() ,
,
当![]() 即
即![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时即
时即![]() 时,
时, ![]() ,
,
此时![]() 在
在![]() 和
和![]() 上都是单调递减的,在
上都是单调递减的,在![]() 上是单调递增的;
上是单调递增的;
(2)(i)![]() ,据题意有
,据题意有![]() ,又
,又![]() ,
,
则![]() 且
且![]() ,
, ![]() ,
,
法1: ![]() ,
,
当且仅当![]() 即
即![]() ,
, ![]() 时取等号.
时取等号.
法2: ![]() ,
, 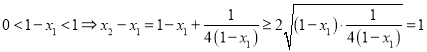 ,
,
当且仅当![]() 时取等号.
时取等号.
(ii)要在点![]() 处的切线重合,首先需要在点
处的切线重合,首先需要在点![]() 处的切线的斜率相等,
处的切线的斜率相等,
而![]() 时,
时, ![]() ,则必有
,则必有![]() ,即
,即![]() ,
, ![]() ,
,
![]() 处的切线方程是:
处的切线方程是: ![]()
![]() 处的切线方程是:
处的切线方程是: ![]() ,
,
即![]() ,
,
据题意则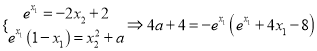 ,
, ![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,
, ![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上单调递增
上单调递增![]() ,
,
则![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,再设
,再设![]() ,
, ![]() ,
,
![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
则![]() 在
在![]() 恒成立,
恒成立,
即当![]() 时,
时, ![]() 的值域是
的值域是![]() ,
,
故![]() ,即为所求.
,即为所求.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目