题目内容
20．
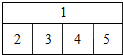用4种不同的颜色填涂如图所示的1，2，3，4，5五个区域，要求一区一色，邻区异色，则不同的填涂方法种数是（ ）| A． | 120 | B． | 96 | C． | 72 | D． | 48 |
分析 先涂区域1有4种方法，区域2有3种涂色方法，区域3有2种涂色方法，区域4有2种涂色方法，区域5有2种涂色方法，根据分步计数原理问题得以解决．
解答 解：先涂区域1有4种方法，区域2有3种涂色方法，区域3有2种涂色方法，区域4有2种涂色方法，区域5有2种涂色方法，根据分步计数原理，得到共有4×3×2×2×2=96种．
故选：B．
点评 本题考查了分步计数原理，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
10．已知直线l经过点P（3，4）．
（1）若直线l的倾斜角为θ（θ≠90°），且直线l经过另外一点（cosθ，sinθ），求此时直线的方程；
（2）若直线l与两坐标轴围成等腰直角三角形，求直线l的方程．
（1）若直线l的倾斜角为θ（θ≠90°），且直线l经过另外一点（cosθ，sinθ），求此时直线的方程；
（2）若直线l与两坐标轴围成等腰直角三角形，求直线l的方程．
11．设f（x）=x2+bx+c，且f（-1）=f（3），则（ ）
| A． | f（1）＞c＞f（-1） | B． | f（1）＜c＜f（-1） | C． | f（1）＞f（-1）＞c | D． | f（1）＜f（-1）＜c |
如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE．若M为线段A1C的中点，则在△ADE翻折过程中，下列命题正确的是①②④．（写出所有正确的命题的编号）