题目内容
5.设$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$是任意非零的平面向量,且互不共线,给出下面的五个命题:(1)|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|; (2)($\overrightarrow{b}$•$\overrightarrow{c}$)$\overrightarrow{a}$-($\overrightarrow{c}$•$\overrightarrow{a}$)$\overrightarrow{b}$不与向量$\overrightarrow{c}$垂直.;
(3)|$\overrightarrow{a}$|-|$\overrightarrow{b}$|<|$\overrightarrow{a}$-$\overrightarrow{b}$|; (4)若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$=0,或者$\overrightarrow{b}$=0;
(5)($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=($\overrightarrow{b}$•$\overrightarrow{c}$)$\overrightarrow{a}$; (6)(3$\overrightarrow{a}$+2$\overrightarrow{b}$)•(3$\overrightarrow{a}$-2$\overrightarrow{b}$)=9|$\overrightarrow{a}$|2-4|$\overrightarrow{b}$|2
其中真命题的序号为(3)(6).
分析 根据向量的模,向量的数量积运算法则,向量垂直的充要条件等知识点逐一判断6个结论的真假,可得答案.
解答 解:(1)中,向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,故cosθ≠±1,|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•|cosθ|≠|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,故(1)错误;
(2)[($\overrightarrow{b}$•$\overrightarrow{c}$)•$\overrightarrow{a}$-($\overrightarrow{c}$•$\overrightarrow{a}$)•$\overrightarrow{b}$]•$\overrightarrow{c}$=($\overrightarrow{b}$•$\overrightarrow{c}$)•($\overrightarrow{a}$•$\overrightarrow{c}$)-($\overrightarrow{c}$•$\overrightarrow{a}$)•($\overrightarrow{b}$•$\overrightarrow{c}$)=0,故($\overrightarrow{b}$•$\overrightarrow{c}$)•$\overrightarrow{a}$-($\overrightarrow{c}$•$\overrightarrow{a}$)•$\overrightarrow{b}$与向量$\overrightarrow{c}$垂直,故(3)错误;
(3)根据三角形两边之差小于第三边,可得|$\overrightarrow{a}$|-|$\overrightarrow{b}$|<|$\overrightarrow{a}$-$\overrightarrow{b}$|,故(3)正确;
(4)若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$=$\overrightarrow{0}$,或者$\overrightarrow{b}$=$\overrightarrow{0}$,或者$\overrightarrow{a}$⊥$\overrightarrow{b}$,故(4)错误;
(5)($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$表示一个与$\overrightarrow{c}$共线的向量,($\overrightarrow{b}$•$\overrightarrow{c}$)•$\overrightarrow{a}$表示一个与$\overrightarrow{a}$共线的向量,当$\overrightarrow{a}$与$\overrightarrow{c}$不共线时,两者一定不相等,故(5)错误;
(6)(3$\overrightarrow{a}$+2$\overrightarrow{b}$)•(3$\overrightarrow{a}$-2$\overrightarrow{b}$)=9$\overrightarrow{a}$2-4$\overrightarrow{b}$2=9|$\overrightarrow{a}$|2-4|$\overrightarrow{b}$|2.故(6)正确;
故真命题的序号为:(6),
故答案为:(3)(6)
点评 本题以命题的真假判断为载体考查了向量的基本运算,难度不大,属于基础题.

| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰直角三角形 |
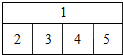 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )| A. | 120 | B. | 96 | C. | 72 | D. | 48 |
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
| A. | 三点确定一个平面 | |
| B. | 四边形一定是平面图形 | |
| C. | 梯形一定是平面图形 | |
| D. | 两条直线没有公共点,则这两条直线平行 |