题目内容
15.已知命题p:方程x2+mx+1=0有两个不相等的实根;q:不等式4x2+4(m-2)x+1>0的解集为R.(1)若命题q为真,求实数m的取值范围.
(2)若命题“p且q”和“非p”为假,求实数m的取值范围.
分析 (1)通过q为真,利用判别式小于0,即可求实数m的取值范围;
(2)通过p为真,利用判别式即可求实数m的取值范围;通过“p且q”和“非p”得到p真q假,求出求实数m的取值范围.
解答 解:(1)因为不等式4x 2+4(m-2)x+1>0的解集为R,
所以△2=16(m-2)2-16<0,
∴1<m<3,
∴若q为真,实数m的取值范围是(1,3).
(2)∵方程x 2+mx+1=0有两个不相等的实根,
所以△1=m 2-4>0,
∴m>2或m<-2,
∴若p为真,实数m的取值范围是(-∞,-2)∪(2,+∞).
∵“p且q”和“非p”为假,
∴p真q假,$\left\{\begin{array}{l}{m>2或m<-2}\\{m≤1或m≥3}\end{array}\right.$,
解得m<-2,或m≥3.
点评 本题考查命题的真假的判断与应用,考查分类讨论思想的应用,考查计算能力.

练习册系列答案
相关题目
20.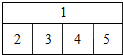 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )| A. | 120 | B. | 96 | C. | 72 | D. | 48 |
 函数y=tan($\frac{π}{4}$x-$\frac{π}{2}$)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$等于( )
函数y=tan($\frac{π}{4}$x-$\frac{π}{2}$)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$等于( )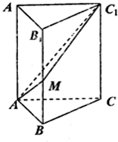 如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.
如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.