题目内容
9. 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列命题正确的是①②④.(写出所有正确的命题的编号)
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列命题正确的是①②④.(写出所有正确的命题的编号)①线段BM的长是定值;
②点M在某个球面上运动;
③存在某个位置,使DE⊥A1C;
④存在某个位置,使MB∥平面A1DE.
分析 取CD中点F,连接MF,BF,则平面MBF∥平面A1DE,可得④正确;由余弦定理可得MB2=MF2+FB2-2MF•FB•cos∠MFB,所以MB是定值,M是在以B为球心,MB为半径的球上,可得①②正确.A1C在平面ABCD中的射影为AC,AC与DE不垂直,可得③不正确.
解答 解:①取CD中点F,连接MF,BF,则MF∥DA1,BF∥DE,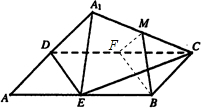
∴平面MBF∥平面A1DE,
∴MB∥平面A1DE,故D正确
由∠A1DE=∠MFB,MF=$\frac{1}{2}$A1D=定值,FB=DE=定值,
由余弦定理可得MB2=MF2+FB2-2MF•FB•cos∠MFB,所以MB是定值,故①正确.
②∵B是定点,
∴M是在以B为球心,MB为半径的球上,故②正确,
若③成立,则由 DE⊥CE,可得 DE⊥面A1EC
∴DE⊥A1E,而这与DA1⊥A1E矛盾
故③错误.
④取CD中点F,连接MF,BF,则平面MBF∥平面A1DE,可得④正确;
故正确的命题有:①②④,
故答案为:①②④.
点评 掌握线面、面面平行与垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
20.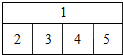 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )| A. | 120 | B. | 96 | C. | 72 | D. | 48 |
14.下列说法正确的是( )
| A. | 三点确定一个平面 | |
| B. | 四边形一定是平面图形 | |
| C. | 梯形一定是平面图形 | |
| D. | 两条直线没有公共点,则这两条直线平行 |
1.复数$\frac{2i}{1-i}$的虚部是( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
19.“指数函数y=ax(a>1)是增函数,y=xα(α>1)是指数函数,所以y=xα(α>1)是增函数”,在以上演绎推理中,下列说法正确的是( )
| A. | 推理完全正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 推理形式不正确 |
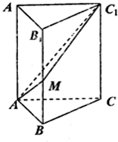 如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.
如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.