题目内容
10.若函数f(x)=-2x+sinx,则满足不等式f(2m2-m+π-1)≥-2π的m的取值范围为[$-\frac{1}{2},1$].分析 f(-x)=2x-sinx=-f(x),所以f(x)为奇函数,f′(x)=-2+cosx≤0,所以f(x)在定义域R为减函数,根据函数的单调性将函数转化为不等式求解.
解答 解:f(-x)=2x-sinx=-f(x),所以f(x)为奇函数,f′(x)=-2+cosx≤0,所以f(x)在定义域R为减函数.
又f(π)=-2π+sinπ=-2π,所以f(2m2-m+π-1)≥-2π可转化为f(2m2-m+π-1)≥f(π).
根据函数的单调性可知,2m2-m+π-1≤π
即2m2-m+-1≤0
解得$m∈[-\frac{1}{2},1]$
故答案为:[$-\frac{1}{2},1$]
点评 本题主要考查函数的单调性和奇偶性的性质应用,属于中档题型.

练习册系列答案
相关题目
20.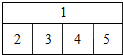 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )| A. | 120 | B. | 96 | C. | 72 | D. | 48 |
1.复数$\frac{2i}{1-i}$的虚部是( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
19.“指数函数y=ax(a>1)是增函数,y=xα(α>1)是指数函数,所以y=xα(α>1)是增函数”,在以上演绎推理中,下列说法正确的是( )
| A. | 推理完全正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 推理形式不正确 |
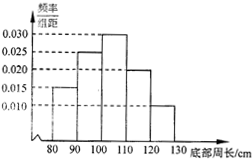 为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.
为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.