题目内容
8.(1)计算$\frac{{{{(1+i)}^2}}}{1+2i}+\frac{{{{(1-i)}^2}}}{2-i}$;(2)若实数x,y满足$\frac{x}{1+i}+\frac{y}{1+2i}=\frac{10}{1+3i}$,求x,y的值.
分析 (1)利用复数的运算法则化简即可;
(2)化简等式左边,利用复数相等,得到关于x,y的方程组解之.
解答 解:(1)$\frac{{{{(1+i)}^2}}}{1+2i}+\frac{{{{(1-i)}^2}}}{2-i}$=$\frac{2i(1-2i)}{(1+2i)(1-2i)}+\frac{-2i(2+i)}{(2-i)(2+i)}$=$\frac{4+2i}{5}+\frac{2-4i}{5}$=$\frac{6-2i}{5}$=$\frac{6}{5}-\frac{2}{5}i$; …(7分)
?(2)$\frac{x}{1+i}+\frac{y}{1+2i}=\frac{10}{1+3i}$⇒$\frac{x(1-i)}{(1+i)(1-i)}+\frac{y(1-2i)}{(1+2i)(1-2i)}=\frac{10(1-3i)}{(1+3i)(1-3i)}$
⇒$\frac{x(1-i)}{2}+\frac{y(1-2i)}{5}=\frac{10(1-3i)}{10}$
⇒$(\frac{x}{2}+\frac{y}{5})-(\frac{x}{2}+\frac{2y}{5})i=1-3i$
∴$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{5}=1}\\{\frac{x}{2}+\frac{2y}{5}=3}\end{array}\right.$
解得x=-2,y=10 …(14分)
点评 本题考查了复数的混合运算以及利用复数相等求参数.考查了学生的运算能力,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知:在△ABC中,acosB=bcosA,则此三角形的形状为( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰直角三角形 |
20.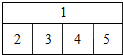 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
 用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )
用4种不同的颜色填涂如图所示的1,2,3,4,5五个区域,要求一区一色,邻区异色,则不同的填涂方法种数是( )| A. | 120 | B. | 96 | C. | 72 | D. | 48 |