题目内容
已知数列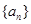 的前
的前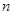 项和
项和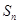 和通项
和通项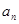 满足
满足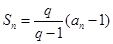 (
(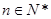 ,
,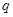 是大于0的常数,且
是大于0的常数,且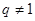 ),数列
),数列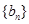 是公比不为
是公比不为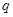 的等比数列,
的等比数列,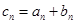 .
.
(1)求数列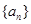 的通项公式;
的通项公式;
(2)设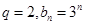 ,是否存在实数
,是否存在实数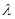 ,使数列
,使数列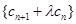 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数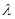 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)数列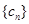 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的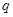 和
和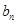 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.
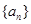 的前
的前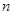 项和
项和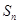 和通项
和通项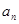 满足
满足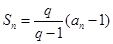 (
(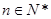 ,
,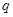 是大于0的常数,且
是大于0的常数,且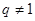 ),数列
),数列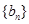 是公比不为
是公比不为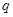 的等比数列,
的等比数列,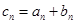 .
.(1)求数列
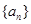 的通项公式;
的通项公式;(2)设
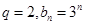 ,是否存在实数
,是否存在实数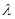 ,使数列
,使数列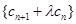 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数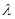 的值,若不存在说明理由;
的值,若不存在说明理由;(3)数列
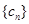 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的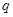 和
和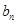 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.(1)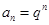 ,(2)λ= 2或λ= 3,(3)不可能为等比数列.
,(2)λ= 2或λ= 3,(3)不可能为等比数列.
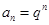 ,(2)λ= 2或λ= 3,(3)不可能为等比数列.
,(2)λ= 2或λ= 3,(3)不可能为等比数列.试题分析:(1)求一般数列通项,常利用和项与通项关系,即当
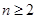 时,
时, 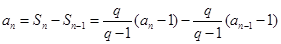 ,整理得
,整理得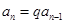 ,又由
,又由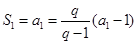 ,得
,得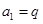 ,
,结合q>0知,数列
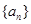 是首项为q公比为
是首项为q公比为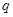 的等比数列, ∴
的等比数列, ∴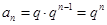 (2)存在性问题,一般从假设存在出发,探求等量关系,将是否存在转化为是否有解. 结合(1)知,当q=2时,
(2)存在性问题,一般从假设存在出发,探求等量关系,将是否存在转化为是否有解. 结合(1)知,当q=2时,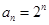 ,所以
,所以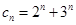 ,假设存在实数
,假设存在实数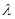 ,使数列
,使数列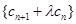 是等比数列,则对任意n≥2有(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn 1),将cn=2n+3n代入上式,整理得
是等比数列,则对任意n≥2有(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn 1),将cn=2n+3n代入上式,整理得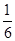 (2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3.(3)首先利用特殊值探讨,得出结论是数列
(2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3.(3)首先利用特殊值探讨,得出结论是数列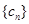 不可能为等比数列.说明也可根据特例. 由题意得c1c3 c22=b1q(p2+q2 2pq),由于p≠q时,p2+q2>2pq,又q及等比数列的首项b1均不为零,所以 c1c3 c22≠0,即 c22≠c1·c3. 故{cn}不是等比数列.
不可能为等比数列.说明也可根据特例. 由题意得c1c3 c22=b1q(p2+q2 2pq),由于p≠q时,p2+q2>2pq,又q及等比数列的首项b1均不为零,所以 c1c3 c22≠0,即 c22≠c1·c3. 故{cn}不是等比数列.解:(1)当
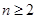 时,
时,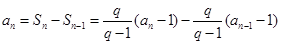 ,整理得
,整理得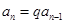 2分
2分又由
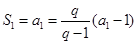 ,得
,得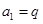 3分
3分结合q>0知,数列
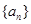 是首项为q公比为
是首项为q公比为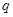 的等比数列, ∴
的等比数列, ∴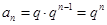 5分
5分(2)结合(1)知,当q=2时,
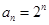 ,所以
,所以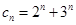 6分
6分假设存在实数
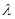 ,使数列
,使数列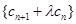 是等比数列,则对任意n≥2有
是等比数列,则对任意n≥2有(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn 1),将cn=2n+3n代入上式,得:
[2n+1+3n+1+λ(2n+3n)]2=[2n+2+3n+2+λ(2n+1+3n+1)]·[2n+3n+λ(2n 1+3n 1)],
即 [(2+λ)2n+(3+λ)3n]2=[(2+λ)2n+1+(3+λ)3n+1][(2+λ)2n 1+(3+λ)3n 1],
整理得
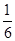 (2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3. 10分
(2+λ)(3+λ)·2n·3n=0,解得λ= 2或λ= 3. 10分故存在实数实数
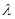 = 2或 3,使数列
= 2或 3,使数列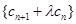 是等比数列. 11分
是等比数列. 11分(3)数列
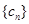 不可能为等比数列. 12分
不可能为等比数列. 12分理由如下:
设等比数列{bn}的公比为p,则由题设知p≠q,则cn=qn+b1pn 1
为要证{cn}不是等比数列只需证c22≠c1·c3.
事实上,
c22=(q2+b1p)2=q4+2q2b1p+b12p2, ①
c1·c3=(q+b1)(q3+b1p2)=q4+b12p2+b1q(p2+q2), ②
②-①得
c1c3 c22=b1q(p2+q2 2pq)
由于p≠q时,p2+q2>2pq,又q及等比数列的首项b1均不为零,
所以 c1c3 c22≠0,即 c22≠c1·c3. 故{cn}不是等比数列. 16分

练习册系列答案
相关题目
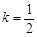 时,数列{an}为递减数列;
时,数列{an}为递减数列;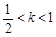 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;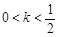 时,数列{an}为递减数列;
时,数列{an}为递减数列;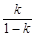 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项. 的首项
的首项 ,
,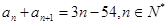
 项和为
项和为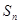 ,求
,求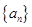 的通项公式为
的通项公式为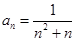 ,其前
,其前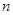 项和为
项和为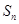 ,则
,则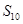 的值为 ( )
的值为 ( )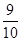
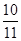
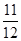
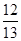
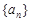 的通项公式
的通项公式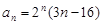 ,则数列
,则数列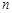 项和
项和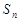 取得最小值时
取得最小值时



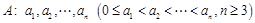 具有性质
具有性质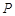 :
: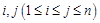 ,
,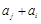 与
与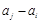 两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列
两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列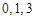 具有性质
具有性质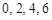 具有性质
具有性质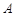 具有性质
具有性质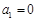 ;
; 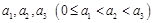 具有性质
具有性质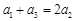 .
. 满足
满足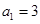 ,
, ,且
,且 ,则
,则
 的前
的前 项和
项和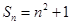 ,则
,则 .
.